LoRA 技术摘要
简介
LoRA(Low-Rank Adaptation of LLMs),即 LLMs 的低秩适应,是参数高效微调最常用的方式之一。属于 PEFT(Parameter-Efficient Fine-Tuning) 的一种方式。
LoRA 的本质就是用更少的训练参数来近似 LLM 全参数微调所得的增量参数,从而减少内存的占用。
原理
对 LLM 做微调的结果可以简要地表示为:
\[\mathbf{W} + \Delta \mathbf{W}\]微调可以被视为在原始参数的基础上学习一个增量 $\Delta \mathbf{W}$,对于全参数微调所获得的 $\Delta \mathbf{W}$ ,其维度与原模型相同,所占用的内存几乎与训练时相同(不考虑优化器等差异)。
但我们可以认为此时的 $\Delta \mathbf{W}$ 是低秩的(至少不是满秩),也就是说该矩阵存在大量的冗余,这个其实很好理解,一般做微调时我们使用的训练数据量都比较少,用如此多的参数量来保存实际上属于“杀鸡用牛刀”了。
由此引出 LoRA 的核心理念,就是用更小的矩阵来表示微调参数。
低秩分解
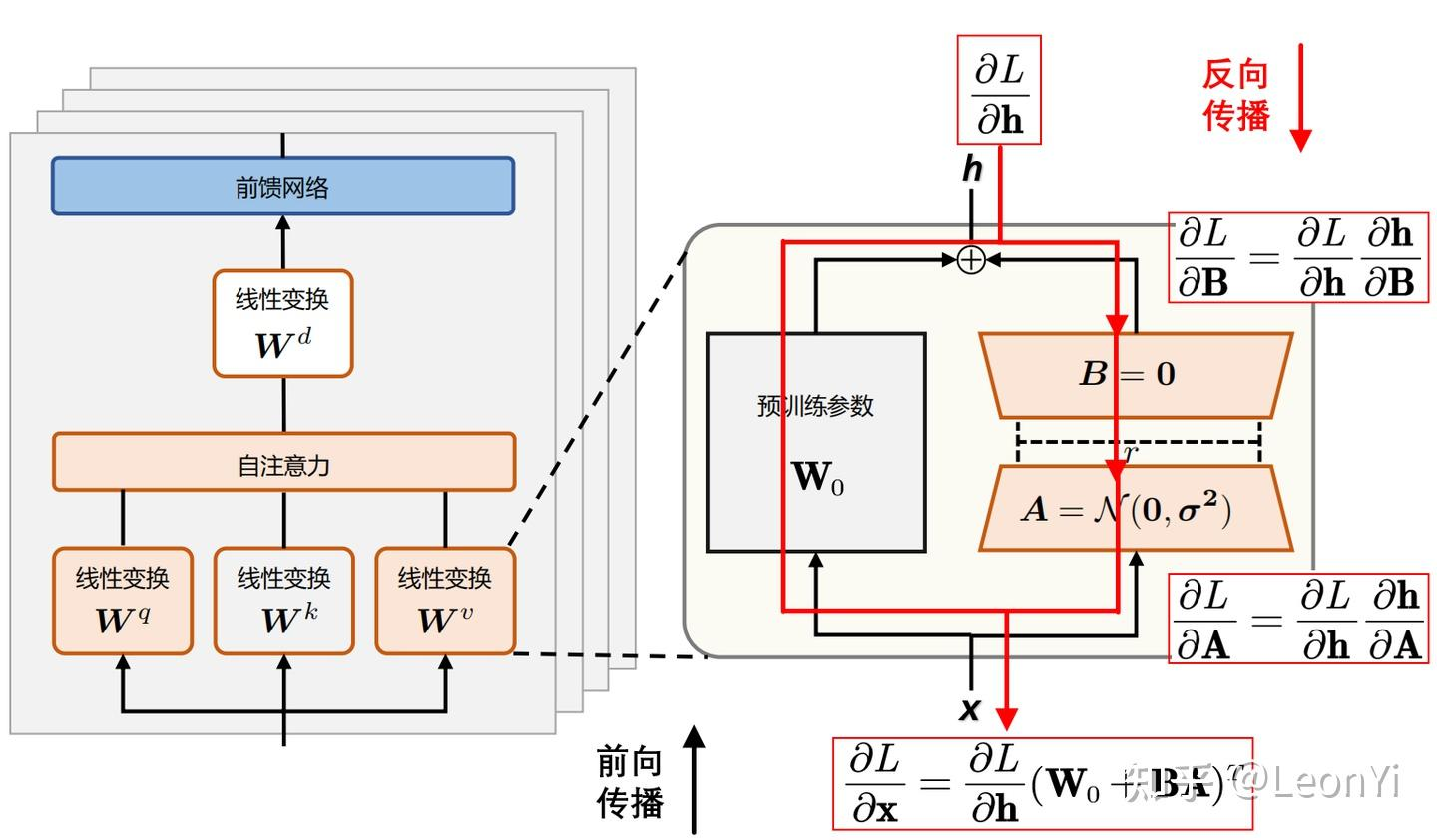
对于预训练权重矩阵 $\mathbf{W}_{0} \in \mathbb{R}^{d \times d} $,LoRA 限制了其更新方式,即将全参微调的增量参数矩阵 $\Delta \mathbf{W}$ 表示为两个参数量更小的矩阵 $\mathbf{B}$ 和 $\mathbf{A}$的低秩近似:
\[\mathbf{W}_{0} + \Delta \mathbf{W} = \mathbf{W}_{0}+ \mathbf{B}\mathbf{A}\]其中,$\mathbf{B}\in \mathbb{R}^{d \times r}$ 和 $\mathbf{A}\in \mathbb{R}^{r \times d}$ 为 LoRA 低秩分解后的权重矩阵,秩 $r$ 远小于 $d$。
参数量直接降为了 2 个 $r * d$,远小于 $d * d$
冻结参数
从本文可知训练时的内存大于推理是主要是因为要保存梯度用于反向传播时更新参数。
LoRA 在微调过程中仅会保存 $\mathbf{A}$ 和 $\mathbf{B}$ 的梯度用于反向传播时的参数更新,而原始模型的参数会被冻结,使其不参与梯度计算,也就无需保存其梯度信息,从而大幅减少了需要计算和存储梯度的参数数量,显著降低了训练所需的内存。
另外还有 $\mathbf{A}$ 和 $\mathbf{B}$ 的参数、梯度和优化器状态上的内存优化,不过和冻结原始模型参数节省的内存比起来都算是小头了。