传输层安全(TLS)相关技术详解
TLS 的目标
传输层安全(TLS)是网络安全的主力。它允许网站向 Web 浏览器证明其身份，并保护所有交换的信息被加密且免受窥探。
TLS 有两个主要目标：保密性和身份验证。两者对于在互联网上进行安全通信都至关重要。保密性主要由密钥安全交换技术和 AES 加密算法实现，身份验证主要由数字签名技术实现
保密性
对称密钥
像 RSA 和 DH 这样的公共关键算法使用大量的 CPU，是 TLS 握手中最慢的部分。笔记本电脑每秒只能执行几百个 RSA 加密，而 AES 对称加密的加密量可达 上千万/秒。
所以应用报文的加密使用的是对称加密技术，而 RSA 和 DH 仅用于对称密钥的交换。
在 TLS 中，这种对称加密通常使用强大的块密码（如AES）完成。较旧的浏览器和平台可能会使用密码，如3DES或流密码RC4，这在现在被认为是不安全的。
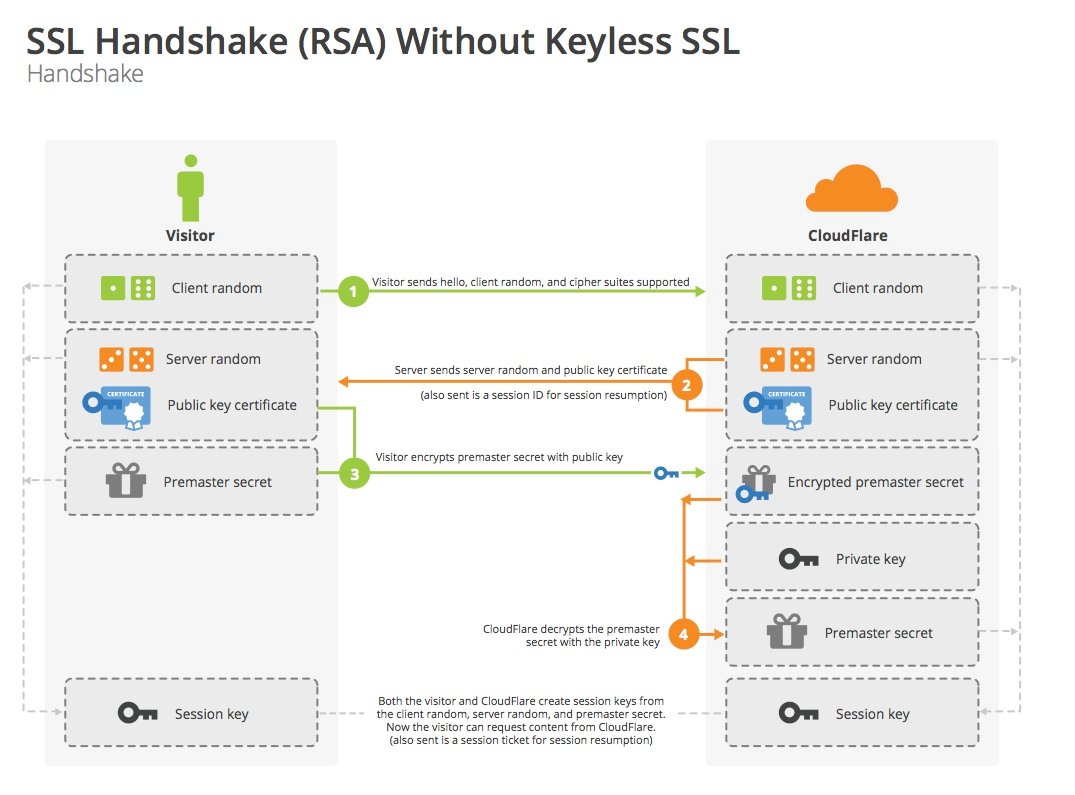
RSA 密钥交换
RSA 密钥交换是目前最主流的密钥交换方式，握手方式如下：
RSA 密钥交换主要是用公钥加密对称密钥后传输，对方用私钥解密的过程
RSA 算法的本质是利用了一个数学原理：将两个大质数相乘非常容易，但要对其乘积进行因式分解却非常困难，详见RSA 加密算法维基百科
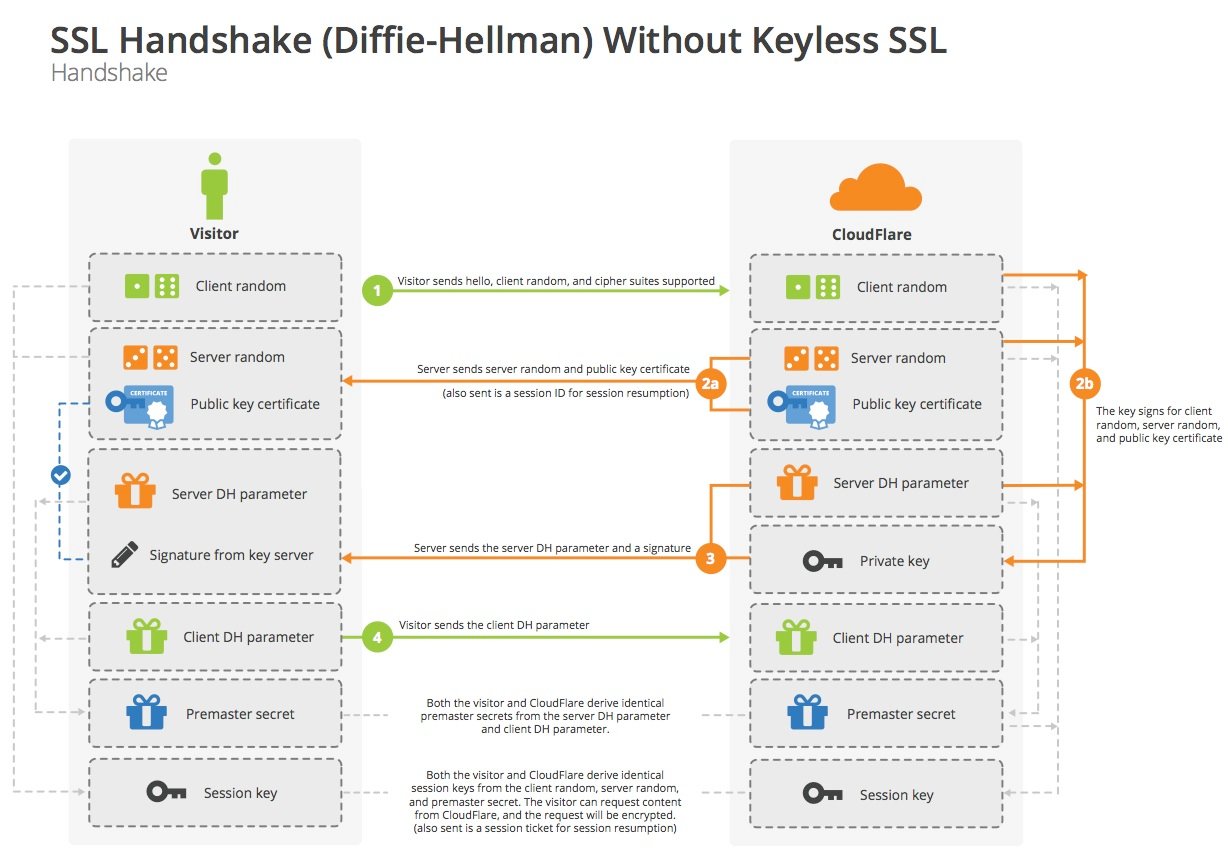
Diffie-Hellman(DH) 密钥交换
DH 算法解决了密钥在双方不直接传递密钥的情况下完成密钥交换，这个神奇的交换原理完全由数学理论支持。
我们来看 DH 算法交换密钥的步骤。假设甲乙双方需要传递对称密钥，他们之间可以这么做：
使用整数的乘法组 modulo p，其中 p 是素数(prime)，g 是 modulo p 的一个原始根(primitive root)。下面是协议的一个示例，非 secret 值用 $\textcolor{blue}{蓝色}$ 表示，secret 值用 $\textcolor{red}{红色}$ 表示。
注意到这个密钥 s 并没有在网络上传输。而通过网络传输的公开的 p，g，A 和 B 是很难推算出 s 的，因为实际算法选择的素数 p 是非常大的(g 不需要很大，通常就 2,3,…)。
所以，更确切地说，DH 算法是一个密钥协商算法，双方最终协商出一个共同的密钥，而这个密钥不会通过网络传输。
DH 算法的安全性
如果已知 g和g^a mod p，要计算出 a是困难的，这就是离散对数问题。离散对数问题被认为是困难的，没有已知的有效算法可以在合理时间内解决它。这种困难性是Diffie-Hellman协议安全性的基础。
正向计算 3^x mod 17 = ？很容易 反向计算 3^? mod 17 = 12 不容易
在 DH 算法握手的过程中，指数不会被传递，也就是说在网络攻击中指数是需要被破解的对象，即使该密钥被暴力破解，也可以通过定期更新密钥的方式大大增加破解工作量
详见Diffie–Hellman key exchange维基百科
DHE 密钥交换
虽然 DH 算法让对称加密的密钥变得足够安全，但私钥还是有被破解的风险，那么干脆就让双方的私钥在每次密钥交换通信时，都是随机生成的、临时的，这个方式也就是 DHE 算法，E 全称是 ephemeral（临时性的）。
ECDHE 密钥交换
DHE 算法使用了大量的乘法运算，导致计算性能不佳，为了提升 DHE 算法的性能，就出现了目前较为流行的密钥交换算法 —— ECDHE 算法。
ECDHE 算法是在 DHE 算法的基础上利用了 ECC 椭圆曲线特性，可以用更少的计算量计算出公钥，以及最终的会话密钥。
椭圆曲线和椭圆其实毫无关系，之所以有“椭圆”两个字，那仅仅是因为其表达式和椭圆周长的积分表达式类似，故此得名。
小红和小明使用 ECDHE 密钥交换算法的过程：
双方事先确定好使用哪种椭圆曲线，和曲线上的基点 G，这两个参数都是公开的；双方各自随机生成一个随机数作为私钥d，并与基点 G相乘得到公钥Q(Q = dG, 具体过程自行研究)，此时小红的公私钥为 Q1 和 d1，小明的公私钥为 Q2 和 d2；双方交换各自的公钥，最后小红计算点(x1，y1) = d1Q2，小明计算点(x2，y2) = d2Q1，由于椭圆曲线上是可以满足乘法交换和结合律，所以 d1Q2 = d1d2G = d2d1G = d2Q1 ，因此双方的 x 坐标是一样的，所以它是共享密钥，也就是会话密钥。
这个过程中，双方的私钥都是随机、临时生成的，都是不公开的，即使根据公开的信息（椭圆曲线、公钥、基点 G）也是很难计算出椭圆曲线上的离散对数（私钥）。
具体算法详见椭圆曲线迪菲-赫尔曼金钥交换维基百科
身份验证
数字签名
RSA 算法和 DH 算法都需要交换公钥，如何保证公钥没有被中间人篡改，也是握手过程中需要解决的问题。
TODO:签名算法涉及的东西也很多，现在还没有学习完，等待后续补充
RSA 签名
常用数字签名算法有：
- MD5withRSA
- SHA1withRSA
- SHA256withRSA
它们实际上就是指定某种哈希算法进行 RSA 签名的方式。
DSA 签名
除了 RSA 可以签名外，还可以使用 DSA 算法进行签名。DSA 是 Digital Signature Algorithm 的缩写，它使用 ElGamal 数字签名算法。
DSA 只能配合 SHA 使用，常用的算法有：
- SHA1withDSA
- SHA256withDSA
- SHA512withDSA
和 RSA 数字签名相比，DSA 的优点是更快。
ECDSA 签名
椭圆曲线签名算法 ECDSA：Elliptic Curve Digital Signature Algorithm 也是一种常用的签名算法，它的特点是可以从私钥推出公钥。比特币的签名算法就采用了 ECDSA 算法，使用标准椭圆曲线 secp256k1。