数据结构--树

二叉树

定义

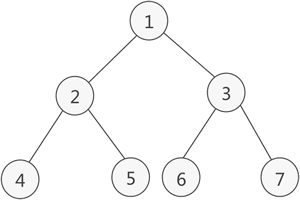
二叉树（英语：Binary tree）是每个结点最多只有两个分支（子树）的树结构。通常分支被称作“左子树”或“右子树”。二叉树的分支具有左右次序，不能随意颠倒。

性质

• 二叉树中，第 $i$ 层最多有 $2^i-1$ 个结点。
• 如果二叉树的深度为 $K$，那么此二叉树最多有 $2^K-1$ 个结点。
• 二叉树中，终端结点数（叶子结点数）为 $n_0$，度为 2 的结点数为 $n_2$，则 $n_0=n_2+1$。

满二叉树

如果二叉树中除了叶子结点，每个结点的度都为 2，则此二叉树称为满二叉树。

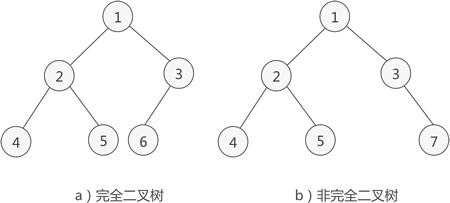
完全二叉树

如果二叉树中除去最后一层结点为满二叉树，且最后一层的结点依次从左到右分布，则此二叉树被称为完全二叉树。

二叉树的顺序存储结构

顺序表

满二叉树或完全二叉树可以使用顺序表表示

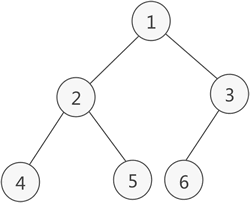
完全二叉树：

顺序表：

可以将非满二叉树转换成满二叉树或完全二叉树，然后用顺序表表示

普通二叉树转为满二叉树：

顺序表：

注意：顺序表图中上排表示结点的值，并不一定是按顺序递增的，下排表示数组索引

寻找左右子结点

• 左结点：$lcIndex = (index + 1)*2 - 1$
• 右结点：$rcIndex = (index + 1)*2$
• 父结点：$fIndex = (index + 1)/2 - 1$

链表

通过链表连接各个结点

结点结构：

还可以添加一个成员表示父结点，构成双向引用

二叉树遍历

深度优先遍历

分作前序遍历、中序遍历、后续遍历，前、中、后代表根节点在遍历时的位置。以下透过 C 语言实作，并均使用递归方法。

可以用于实现深度优先搜索（英语：Depth-First-Search，DFS）

前序遍历

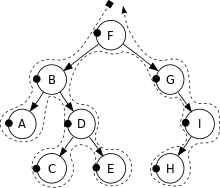
前序遍历（Pre-Order Traversal）是依序以根节点、左节点、右节点为顺序走访的方式。

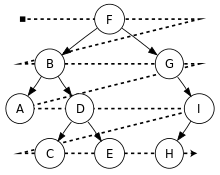
深度优先遍历（前序遍历）F, B, A, D, C, E, G, I, H

注意：虚线经过黑点表示触发读取

void pre_order_traversal(TreeNode *root) {
    // Do Something with root
    if (root->lchild != NULL) //若其中一側的子樹非空則會讀取其子樹
        pre_order_traversal(root->lchild);
    if (root->rchild != NULL) //另一側的子樹也做相同事
        pre_order_traversal(root->rchild);
}

中序遍历

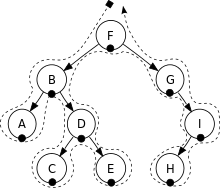
中序遍历（In-Order Traversal）是依序以左节点、根节点、右节点为顺序走访的方式。

深度优先遍历（中序遍历）A, B, C, D, E, F, G, H, I

注意：虚线经过黑点表示触发读取

void in_order_traversal(TreeNode *root) {
    if (root->lchild != NULL) //若其中一側的子樹非空則會讀取其子樹
        in_order_traversal(root->lchild);
    // Do Something with root
    if (root->rchild != NULL) //另一側的子樹也做相同事
        in_order_traversal(root->rchild);
}

后续遍历

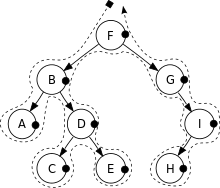
后序遍历（Post-Order Traversal）是依序以左节点、右节点、根节点为顺序走访的方式。

深度优先搜索（后序遍历）：A, C, E, D, B, H, I, G, F

注意：虚线经过黑点表示触发读取

void post_order_traversal(TreeNode *root) {
    if (root->lchild != NULL) //若其中一側的子樹非空則會讀取其子樹
        post_order_traversal(root->lchild);
    if (root->rchild != NULL) //另一側的子樹也做相同事
        post_order_traversal(root->rchild);
    // Do Something with root
}

利用栈取代递归

以中序遍历为例

void in_order(TreeNode *root) {
    stack <TreeNode *> node_stack;
    node_stack.push(root);
    while(!node_stack.empty())
    {
        curr = node_stack.top();
        node_stack.pop();
        // Do Something with root

        if (curr->rchild != NULL)
            node_stack.push(curr->rchild);
        if (curr->lchild != NULL)
            node_stack.push(curr->lchild);
    }
}

广度优先遍历

和深度优先遍历不同，广度优先遍历会先访问离根节点最近的节点。二叉树的广度优先遍历又称按层次遍历。算法借助队列实现。

可以用于实现广度优先搜索（英语：Breadth-First Search，缩写为BFS）

广度优先遍历 - 层次遍历：F, B, G, A, D, I, C, E, H

void level(TreeNode *node)
{
  Queue *queue = initQueue();
  enQueue(queue, node);

  while (!isQueueEmpty(queue))
  {
    // 利用队列的fifo特性依次处理节点
    TreeNode *curr = deQueue(queue);

    // Do Something with curr
    // 比如打印节点的值
    print(curr->value);

    if (curr->lchild != NULL)
      enQueue(queue, curr->lchild);
    if (curr->rchild != NULL)
      enQueue(queue, curr->rchild);
  }
}

二叉查找树

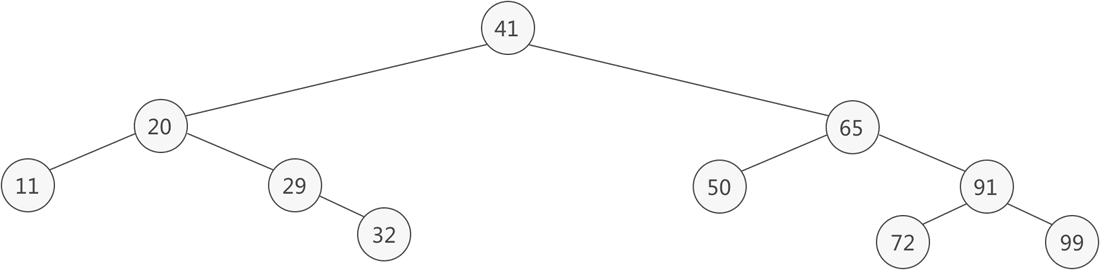
二叉排序树（Binary Sort Tree，简称 BST ）又叫二叉查找树和二叉搜索树，是一种实现动态查找表的树形存储结构。

特性

• 对于树中的每个结点，如果它有左子树，那么左子树上所有结点的值都比该结点小；
• 对于树中的每个结点，如果它有右子树，那么右子树上所有结点的值都比该结点大。

平衡二叉树

平衡二叉(查找)树，又称为 AVL 树

特性

• 每棵子树中的左子树和右子树的深度差不能超过 1；
• 二叉树中每棵子树都要求是平衡二叉树；

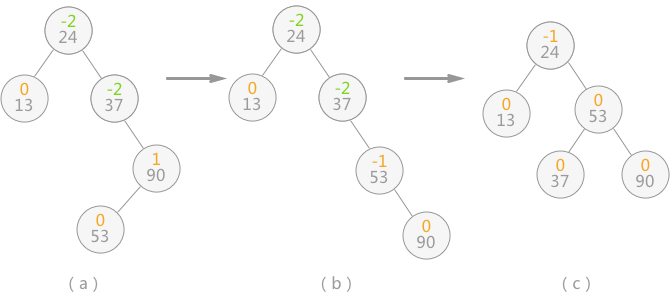
可以通过旋转将非平衡的二叉查找树转化为平衡二叉树：

红黑树

特殊的二叉查找树，并不一定是平衡二叉树，它的统计性能要好于平衡二叉树

特性

1. 结点是红色或黑色。
2. 根结点是黑色。
3. 所有叶子都是黑色。（叶子是 NIL 结点）
4. 每个红色结点的两个子结点都是黑色。（从每个叶子到根的所有路径上不能有两个连续的红色结点）
5. 从任一结点到其每个叶子的所有路径都包含相同数目的黑色结点。

这些约束确保了红黑树的关键特性：从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。结果是这个树大致上是平衡的。因为操作比如插入、删除和查找某个值的最坏情况时间都要求与树的高度成比例，这个在高度上的理论上限允许红黑树在最坏情况下都是高效的，而不同于普通的二叉查找树。

要知道为什么这些性质确保了这个结果，注意到性质4导致了路径不能有两个毗连的红色结点就足够了。最短的可能路径都是黑色结点，最长的可能路径有交替的红色和黑色结点。因为根据性质5所有最长的路径都有相同数目的黑色结点，这就表明了没有路径能多于任何其他路径的两倍长。

• 最短路径：黑-黑-黑，
• 可能路径：黑-红-黑-黑/黑-黑-红-黑，
• 最长路径：黑-红-黑-红-黑（根和叶子必须为黑，红色不能相邻）

在很多树数据结构的表示中，一个结点有可能只有一个子结点，而叶子结点包含数据。用这种范例表示红黑树是可能的，但是这会改变一些性质并使算法复杂。为此，本文中我们使用”nil 叶子”或”空（null）叶子”，如上图所示，它不包含数据而只充当树在此结束的指示。这些结点在绘图中经常被省略，导致了这些树好像同上述原则相矛盾，而实际上不是这样。与此有关的结论是所有结点都有两个子结点，尽管其中的一个或两个可能是空叶子。

多路查找树

区别于二叉查找树，多路查找树的子结点可以超过 2，且必须是满树（子结点数量只能是最大或零）。

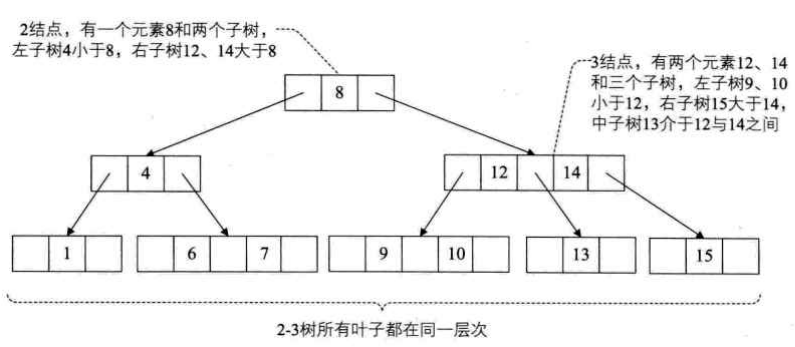
2-3 树

• 子结点数为 2 或 3。
• 一个 2 结点包含一个元素和两个孩子（或没有孩子），且与二叉排序树类似，左子树包含的元素小于该元素，右子树包含的元素大于该元素。不过，与二叉排序树不同的是，这个 2 结点要么没有孩子，要有就有两个，不能只有一个孩子。
• 一个 3 结点包含一小一大两个元素和三个孩子（或没有孩子），一个 3 结点要么没有孩子，要么具有 3 个孩子。如果某个 3 结点有孩子的话，左子树包含小于较小元素的元素，右子树包含大于较大元素的元素，中间子树包含介于两元素之间的元素。
• 2-3 树中所有叶子都在同一层次上。

B 树

B 树（B-Tree，B-树）是一种平衡的多路查找树，结点最大的孩子数目称为 B 树的阶（order），如 2-3 树就是一种 3 阶 B 树

相比于平衡二叉树或红黑树，B 树进一步减少了树的层数，在查找性能上可能不如平衡二叉树，但对于数据的访问次数减少了。我们把读取树中的一个结点视为一次读取操作，层数越少，读取次数就越少。这一点在向硬盘读取时比较重要，通过将一个结点大小和硬盘的页大小匹配，由于硬盘读取是以页为单位的，读页次数会远小于平衡二叉树。

B+ 树

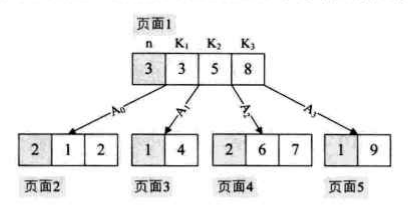
B 树还是有缺陷的，对于树结构来说，可以通过中序遍历(先遍历左子树，然后访问根结点，最后遍历右子树)来顺序查找树中的元素，这一切都是在内存中进行。但是在 B 树中，往返于每个结点就意味着，必须得在硬盘的页面之间进行多次访问，例如，遍历下面这棵 B 树，假设每个结点都属于硬盘的不同页面，中序遍历所有元素就需要访问：页面 2→ 页面 1→ 页面 3→ 页面 1→ 页面 4→ 页面 1→ 页面 5。即每次经过结点遍历时，都会对结点中的元素进行一次遍历，如何让遍历时每个元素只访问一次就成了需要解决的问题。

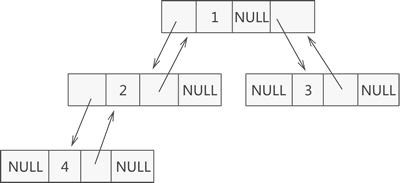
B 树：

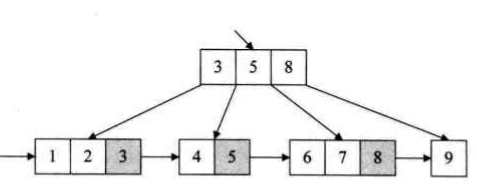
为了更简单的遍历，而产生了 B+ 树。B+ 树是应文件系统所需而出的一种 B 树的变形树，在 B 树中，每一个元素在该树中只出现一次，有可能在叶子结点上，也有可能在分支结点（非叶子结点）上。而在 B+ 树中，出现在分支结点中的元素会被当做它们在该分支结点位置的中序后继者（叶子结点）中再次列出。另外，每一个叶子结点都会保存一个指向后一叶子结点的指针。

B+ 树：

也就是叶子节点包含了所有数据，非叶子节点可以视为只是一种索引（不存放 value，只存放 key）。查找时做法和 B 树一样从根结点开始，继承了该特性；而由于后续指针的存在，遍历时只需遍历所有叶子节点即可。这是一种空间换性能的做法。

二叉堆

二叉堆（英语：binary heap）是一种特殊的堆，二叉堆是完全二叉树或者是近似完全二叉树。

二叉堆满足堆特性：父节点的键值总是保持固定的序关系于任何一个子节点的键值，且每个节点的左子树和右子树都是一个二叉堆

当父节点的键值总是大于或等于任何一个子节点的键值时为“最大堆”。当父节点的键值总是小于或等于任何一个子节点的键值时为“最小堆”。

            1                                 11
         /      \                          /      \
       2         3                       9         10
    /    \     /   \                   /   \     /    \
   4      5   6     7                5      6   7      8
  / \    / \                        / \    / \
 8  9   10 11                      1   2  3   4
        最小堆                              最大堆

可以将这两个堆保存在数组中（完全二叉树的数组表示）：

顶点值:  1  2  3  4  5  6  7  8  9 10 11
最小堆:  1  2  3  4  5  6  7  8  9 10 11
最大堆: 11  9 10  5  6  7  8  1  2  3  4

也可以保存在链表中（完全二叉树的链表表示）

radix 树

radix 树是一种多叉树，是 hash 表(key-value 键值对)的一种实现方式。

核心思想是将 key 切割成多个部分，每部分作为树的一层。树中所有节点都是 key 的组成部分，而叶子节点最终指向 value。

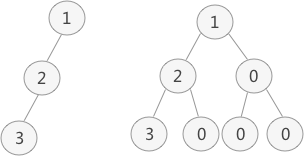
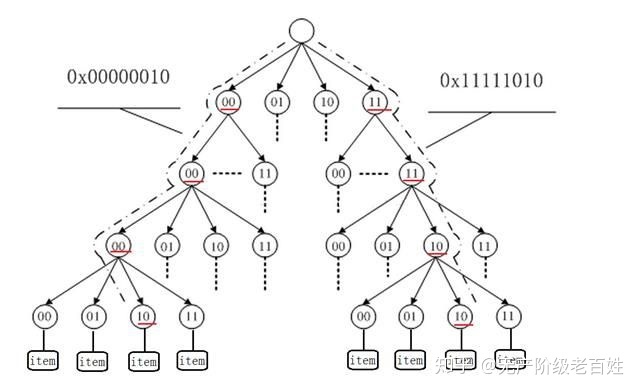
如图是 2 比特的 radix 树，每个节点包含 2 比特的 key，从根开始到叶子的一条路径就是一个 key 值，叶子节点指向该 key 对应的 value

每个节点的比特越多，树的分支就越多，深度就越低。单比特 radix 树就是二叉树。

COSEM协议中的OBIS其实也可以使用该方法来加速查询。

参考

• 平衡二叉树（AVL 树）及 C 语言实现
• 30 张图带你彻底理解红黑树
• 树的遍历