DeepSeek 笔记
架构
DeepSeek V3 的主要架构时一个 Decoder-only 的 Transformer 模型。
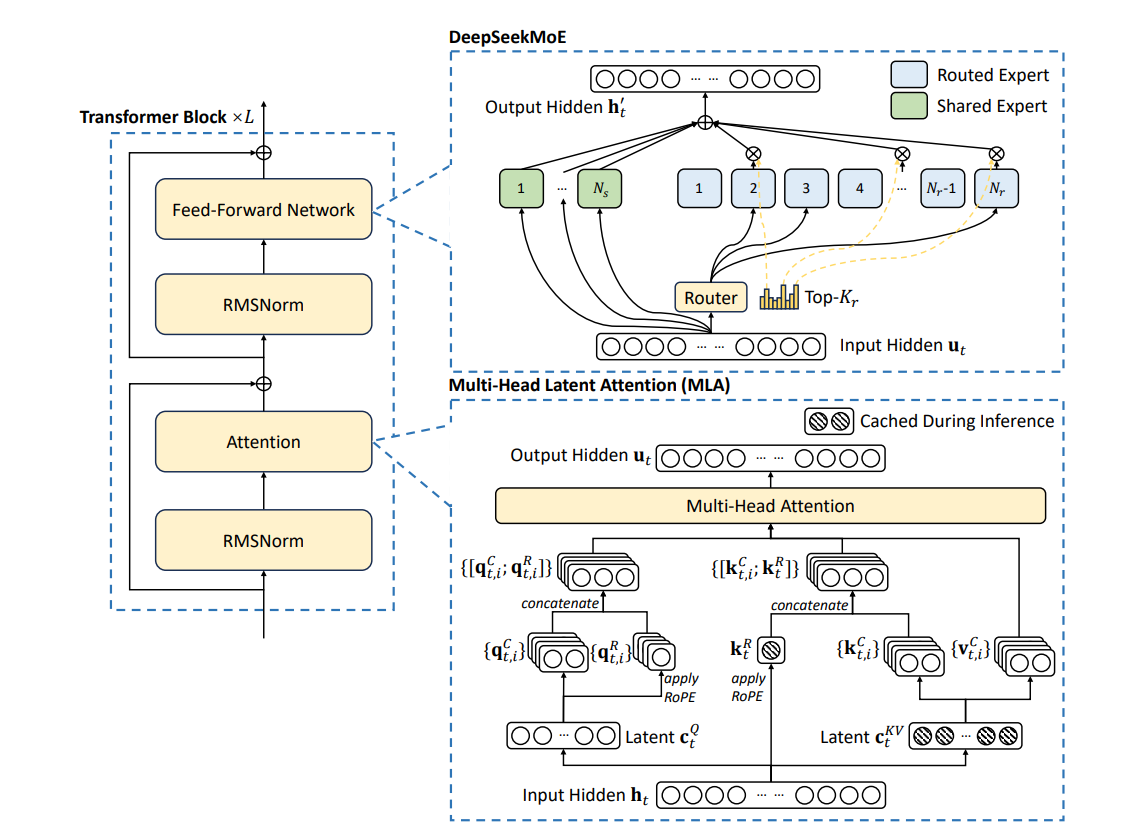
Multi-Head Latent Attention
主要作用是加速推理。
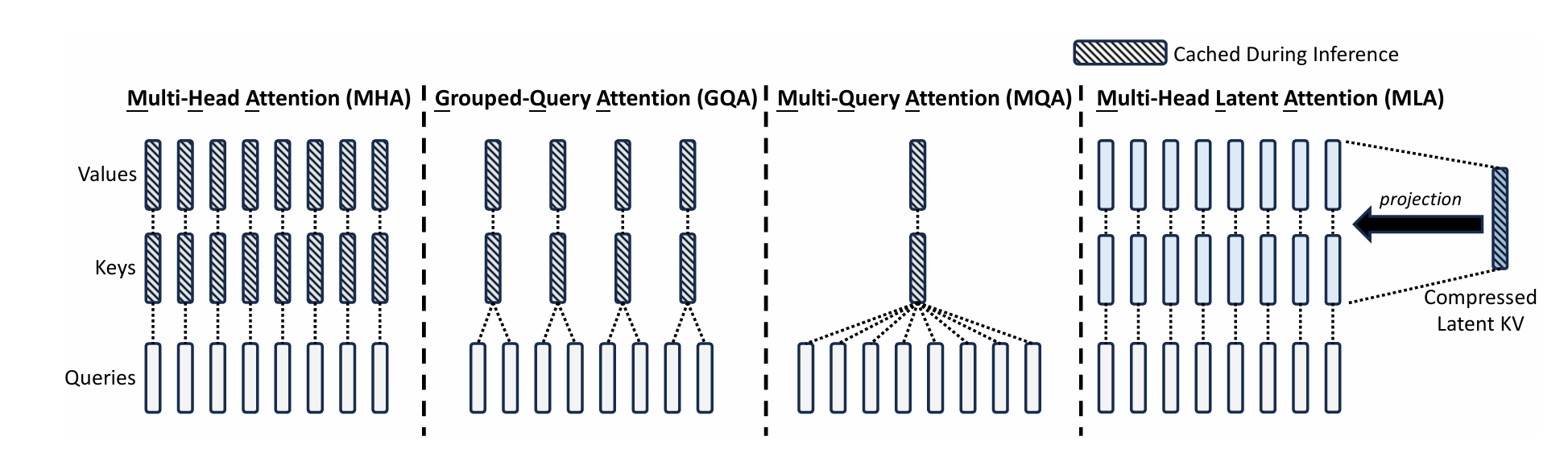
kv cache
在之前的 transformer 架构中,我们了解到 Decoder 实际是一个 auto-regressive 的模型,推理时为了实现 auto-regressive,每个 token 生成时都需要前面所有已经生成的 token 信息,这样就避免不了大量的重复计算。这里的重复计算主要是指 token 变为 key 和 value 的过程,也就是 Embedding 和 Positional Encoding(见Transformer 架构图)。
通过将这些已经生成过的 key 和 value 矩阵保存下来用于之后的推理,也就是 kv cache 的作用。cache 带来如下好处:
- 计算 $k_t$ 可以利用 $k_{t-1}$ 的矩阵,在其上做一次 concatenate 附加当前的 token 计算信息即可,如果 $k_{t-1}$ 已经被缓存也就是无需重复计算,该操作的效率将大大提升。$v_t$ 同理。
- 当推理时遇到相同 $k_t$ 时可以利用之前保存的 cache 而不用重复计算。$v_t$ 同理。
但是这种简单的解决方案无非是空间换时间,带来的问题就是消耗了宝贵的内存。
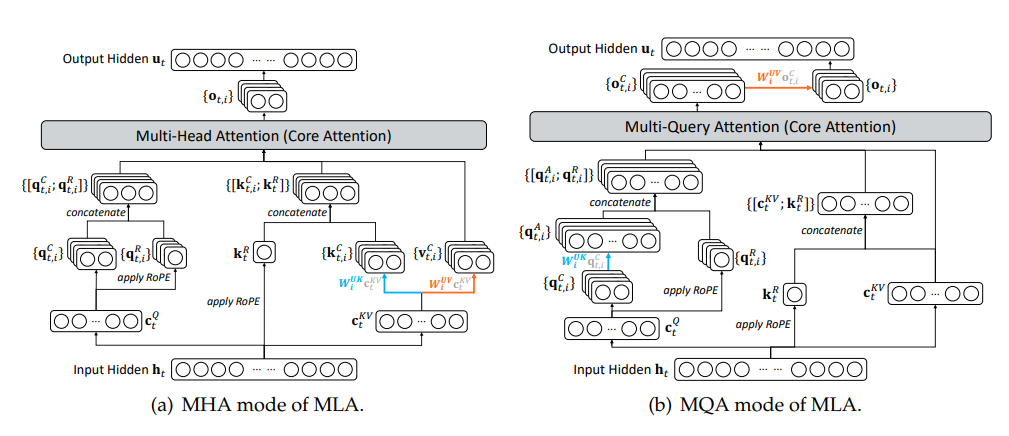
MLA 就是用来解决 MHA 中的 kv cache 过大的问题,原理很简单,原来 Multi-Head Attention 中是把 query、key、value 分别投影到各自的若干个低维空间中(见Multi-Head Attention),假设 $h_t$ 表示输入序列中的第 t 个 token,由 Attention 的理念可知对于 query,key,value 来说这个值是相同的,由 MHA 的定义可知它们的投影的参数($𝑊^{𝑄}$,$𝑊^{K}$,$𝑊^{V}$)不同,所以经过投影后的结果各不相同:
\[q_𝑡 = 𝑊^{𝑄}h_𝑡,\] \[k_𝑡 = 𝑊^{𝐾}h_𝑡,\] \[v_𝑡 = 𝑊^{𝑉}h_𝑡,\] \[[q_{𝑡,1};q_{𝑡,2};\dots;q_{𝑡,𝑛_ℎ}]=q_𝑡,\] \[[k_{𝑡,1};k_{𝑡,2};\dots;k_{𝑡,𝑛_ℎ}]=k_𝑡,\] \[[v_{𝑡,1};v_{𝑡,2};\dots;v_{𝑡,𝑛_ℎ}]=v_𝑡,\]对 MHA 来说每个 head (分维度)的输出计算方式如下(每个 head 使用 $i$ 下标表示, $j$ 下标表示当前的 $q_t$ 需要和 t 位置以及 t 之前所有位置(1 到 t-1)的 key 计算关系,这是 transformer 实现 auto-regressive 的基本机制):
\[\mathbf{o}_{t,i} = \sum_{j=1}^{t} \text{Softmax}_j \left( \frac{\mathbf{q}_{t,i}^T \mathbf{k}_{j,i}}{\sqrt{d_h}} \right) \mathbf{v}_{j,i},\]所有分维度的结果进行整合,得到第 t 个 token 的结果:
\[\mathbf{u}_t = W^O [\mathbf{o}_{t,1}; \mathbf{o}_{t,2}; \dots; \mathbf{o}_{t,n_h}].\]MLA 的设计思路是,此时的 $𝑊^{𝐾}$ 和 $𝑊^{V}$ 中有很多相同的部分,可以再提取它们中相同的部分,这样公用的部分变大,每个 HEAD 特化的部分变小,总体的 cache 就小了:
\[c^{𝐾𝑉}_𝑡 =𝑊^{𝐷𝐾𝑉}h_𝑡,(1)\] \[k^{𝐶}_𝑡 =𝑊^{𝑈𝐾}c^{𝐾𝑉}_𝑡,\] \[v^{𝐶}_𝑡 =𝑊^{𝑈V}c^{𝐾𝑉}_𝑡,\]这里的(1)是将 MHA 的映射和压缩进行了整合,也就是将$h_t$(也就是非 muti-head 的 attention 中的 $k_t$ 或 $v_t$)使用 $𝑊^{𝐷𝐾𝑉}$ 矩阵进行映射+压缩(就是降维,D 就是 down 降维)得到 $c_t$ ($c$ 表示 cache),计算权重时,原表达式中的每个 head(维度)中的 $k_t$ 和 $v_t$ 都可以使用每个 head 对应的解压参数($𝑊^{𝑈𝐾}$ 和 $𝑊^{𝑈V}$) 和 $c_t$ 运算得到(而且 $c_t$ 是 key 和 value 共用的,cache 的占用空间非常小,如上图所示,就是 1/16)。
我们先不考虑 Positional Encoding,在 cache 命中的情况下可以这样计算:
\[\mathbf{o}_{t,i} = \sum_{j=1}^{t} \text{Softmax}_j \left( \frac{\mathbf{q}_{t,i}^T 𝑊^{𝑈𝐾}_{i} c^{𝐾𝑉}_{j}}{\sqrt{d_h}} \right) 𝑊^{𝑈V}_{i} c^{𝐾𝑉}_{j}\]现在考虑 Positional Encoding,这么做就带来了一个问题,MHA 中的 $k_t$ 实际是带了位置信息的(下面的 $k^R_t$,$v_t$ 不带),因为 transformer 架构使用了相对位置,也就是说 $t_1$ 位置的 $k^R_{t_1}$ 会因为当前位置 t 的不同有不同结果,比如在 $t_2 = t_1 + 1$,$t_3 = t_1 + 2$,在 $t_2$ 位置和 $t_3$ 位置计算 $k^R_{t_1}$ 会不同:
\[k^{R}_{t} = RoPE(W^{KR}h_t)\] \[k_{t,i} = [k^{C}_{t,i};k^R_t]\]所以只能去 cache 位置无关的 $k^{C}{t,i}$ ,而 $k^{R}{t}$ 依然要每次去重新计算。
DeepSeek 还对 query 也进行了压缩,方式和对 key 和 value 的压缩相似,主要是用于降低训练时的内存消耗。
总结下:和 MHA 对比, kv cahce 保存的是 $c_t$ 而不是 $k_t$ 和 $v_t$,占用内存更小,但因为即使 cache 命中后也需要做额外的解压操作,性能不如 MHA。
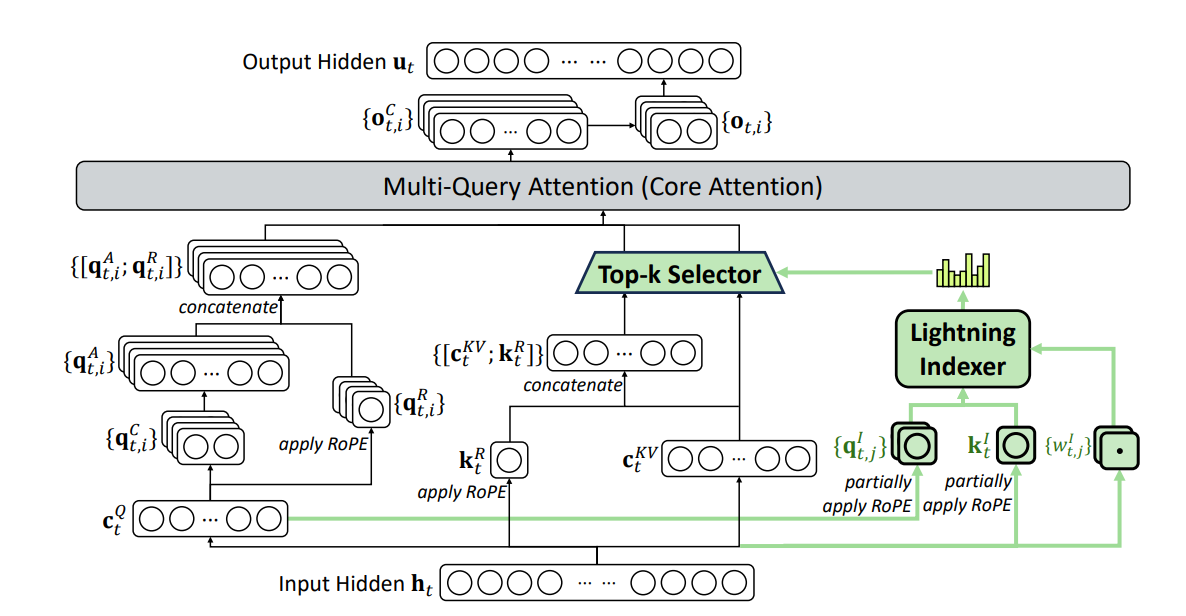
DeepSeek Sparse Attention (DSA)
DeepSeek 在 DeepSeek-V3.2-Exp 中提出了 DeepSeek Sparse Attention (DSA,DeepSeek 稀疏注意力),大幅提高了训练和推理性能,尤其是在长上下文场景中。
在之前的注意力机制中,每个 token 都需要其前后(预测场景只需前面的)所有的 token 做注意力计算,特别是在 MHA 或 MLA 中,计算量更是翻了 HEAD 数量的倍数。其实很多都是没什么用的(最后计算出来的注意力权重很低),稀疏注意力的目的是提前找出有可能权重较低的注意力(q、k、v)让其不参与后续的注意力计算(权重为 0)。
分为两个模块:
- a lightning indexer(快速索引器)
- a fine-grained token selection mechanism(细粒度 token 选择机制)
lightning indexer
作用是获取当前 token 和之前的每个 token 的相关性,可以理解为一种简易的 attention。
\[I_{t,s} = \sum_{j=1}^{H^{I}} w_{t,j}^{I} \cdot \mathrm{ReLU}\left( \mathbf{q}_{t,j}^{I} \cdot \mathbf{k}_{s}^{I} \right)\]首先就是借鉴了 MHA ,增加维度,其中:
- $H^I$ 表示 HEAD 数量,通过映射到多个低维空间再整合增加可训练的参数量和泛化能力
- $w$ 表示可以训练的参数,每个 HEAD 都有一个
- $q_{t,j}^I \cdot k_s^I$ 表示每个 HEAD 上的 query 和历史的 key(HEAD 无关) 的关联,ReLU 函数把小于某个值的关联直接视为无关联,表示我们并不关心关联较小的情况
将每个 HEAD 的计算结果相加,这样我们就得到了当前 token 对应的 $h_t$ 和之前的某一个 $h_s$ 的关联度 $I_{t,s}$,我们计算 $h_t$ 和每一个之前 $h_s$ 的关联度,可以得到它们的关联关系。
这里的 HEAD 数量要比 MHA 或 MLA 中的小,而且可以用 FP8 来表示,性能会高很多。
fine-grained token selection mechanism
有了之前的 lightning indexer 的计算结果,在计算 attention 时,就能过滤掉我们不关心的那些关联度较小的 $h_s$:
\[\mathbf{u}_t = \mathrm{Attn}\left( \mathbf{h}_{t}, \{ \mathbf{c}_s \mid I_{t,s} \in \mathrm{Top\_k}(I_{t,:}) \} \right)\]节省掉的计算量远大于 lightning indexer 增加的计算量。
Multi-Query Attention(MQA) mode
基于 MQA 的 MLA 比基于 MHA 的更加适合应用 DSA:
专家负载均衡
专家模型(MoE)
专家模型作用于 Transformer 模型中的 Feed-Forward Networks(FFN) 层,是为了应对 FFN 层中参数量过大的问题的。
MoE 首先将 FFN 分为好几个不同的部分,称为专家,总体架构分为两类:
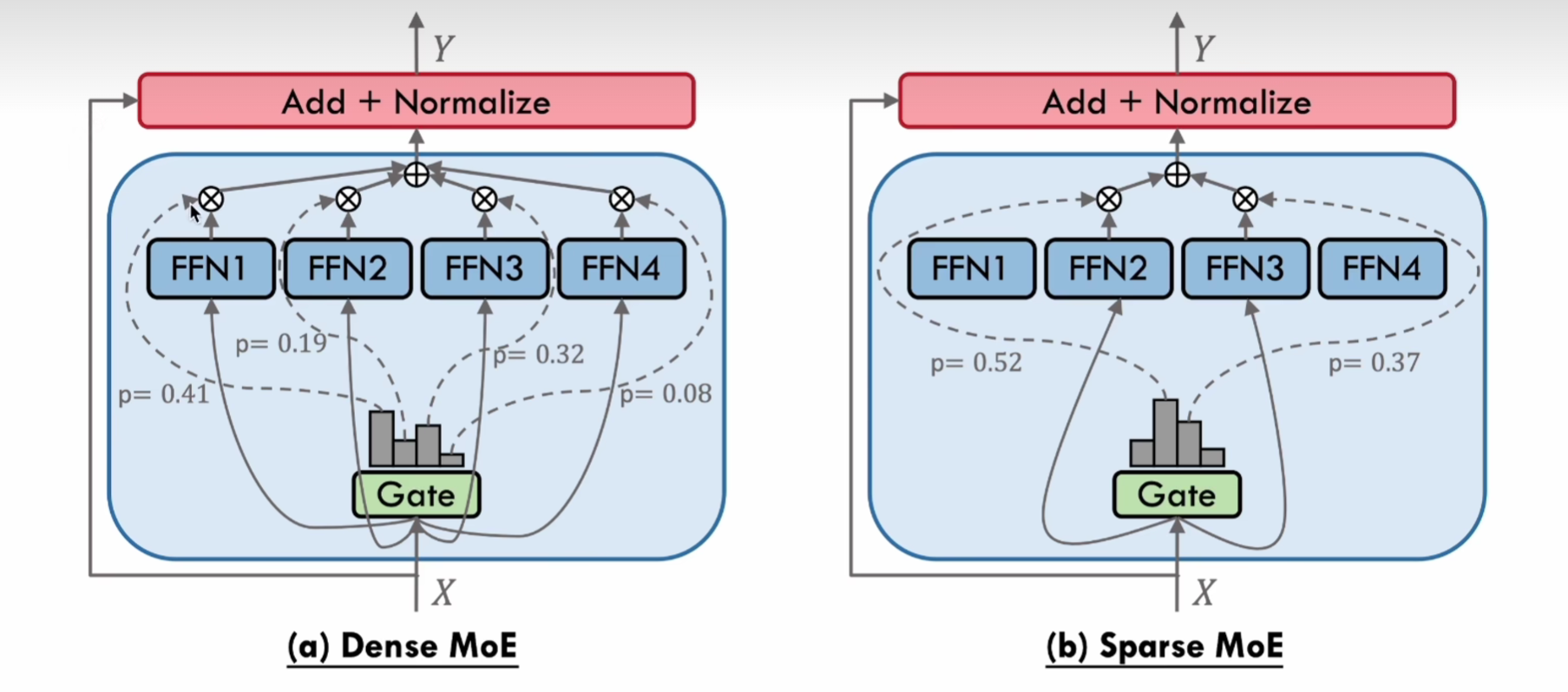
- Dense MoE:将数据输入所有的 FFN 做处理,再对结果做加权平均
- Sparse MoE:考虑到 FFN 层的处理实际上也会占用一定的计算量,所以只选取 topK 个专家处理数据,比如图中仅选取了 FFN2 和 FFN3,忽略掉关联关系不大的专家
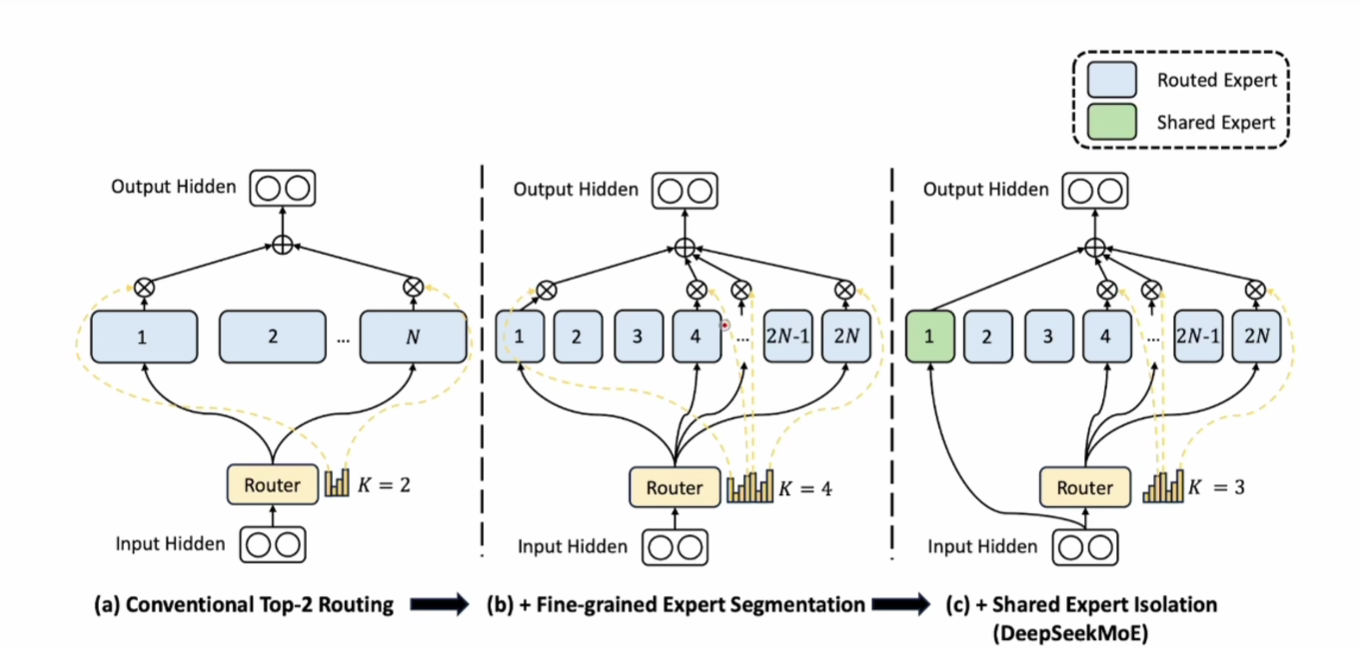
DeepSeekMoE
DeepSeekMoE 并没有什么特别之处,只是将专家数量增加并减少每个专家的参数量,以及增加了 Shared Expert 概念,这个专家处理常识,所有问题都一定会经过这个专家。另外的可以称为 Router Expert。
计算输出的表达式如下:
\[\mathbf{h}'_t = \mathbf{u}_t + \sum_{i=1}^{N_s} \text{FFN}^{(s)}_i(\mathbf{u}_t) + \sum_{i=1}^{N_r} g_{i,t} \, \text{FFN}^{(r)}_i(\mathbf{u}_t)\]上式中,$u_t$ 表示输入向量,第一部分是输入本身,也就是残差连接,第二部分是 Shared Expert 的和,第三部分是 Router Expert 的加权和。
\[g_{i,t} = \frac{g'_{i,t}}{\sum_{j=1}^{N_r} g'_{j,t}}\] \[g'_{i,t} = \begin{cases} s_{i,t}, & \text{if } s_{i,t} \in \text{TopK}\left( \{ s_{j,t} \mid 1 \leq j \leq N_r \},\, K_r \right), \\ 0, & \text{otherwise}. \end{cases}\]上式表示只选取 TopK 个 Router Expert,其他的路由不选择
\[s_{i,t} = \text{Sigmoid}\left( \mathbf{u}_t^\top \mathbf{e}_i \right)\]上式中的 $s_{i,t}$ 就是亲和度(或叫权重)的计算方式,核心就是这个 $e_i$ 向量,表示每个专家的独有的 “代表向量”。
MoE loss
MoE 的一大问题时如何避免单个专家过拟合,也就是一个专家被训练的 token 远大于其他专家,也就是 Gate 或 Router 的分配不均衡。要解决的问题就是专家负载均衡。
一种方式就是将分配策略也加入结果 loss 计算中(Auxiliary Load-Balancing Loss),参考 switch transformer,通过让 loss 最小就能自然而然的得到最优的分配策略
DeepSeek 提出的方法称为 Auxiliary-Loss-Free Load Balancing,也就是动态调整路由,但不将其作为模型的参数,仅影响选择 topK 的策略,不会影响权重计算:
\[g'_{i,t} = \begin{cases} s_{i,t}, & \text{if } s_{i,t} + b_i \in \text{TopK}\left(\{s_{j,t} + b_j \mid 1 \leq j \leq N_r\},\, K_r\right), \\ 0, & \text{otherwise}. \end{cases}\]从式子中看出,计算出专家的权重后,增加了一个动态的 b 偏置,当监测到这个专家在之前的训练中收到了过多的 token , b 就会减少来让该专家的动态权重变小,减少其被选择的概率。最后计算加权平均时,这个实际权重并不包含 b。最后的推理过程不会包含这个 b。
Node-Limited Routing
DeepSeekMoE 的另一大改进是将其中的每个 Router Expert 绑定给了固定的几个 GPU Node,因为数据在 GPU Node 间拷贝的消耗是很高的,通过限制 Expert 的运行范围,减少了拷贝。
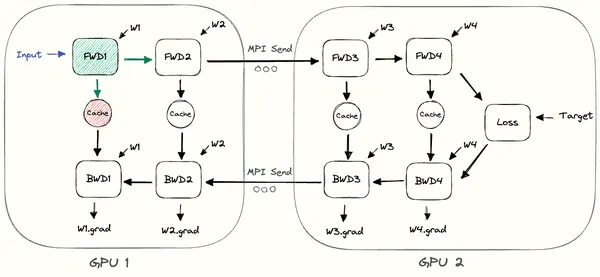
多节点间的前向和反向传播(pipeline parallel 流水线并行):
数据就像流水线一样在不同节点间通过,每个节点处理完一个数据就可以立即处理下一个数据,就像工厂里的流水线一样,每道工序都饱和运转。
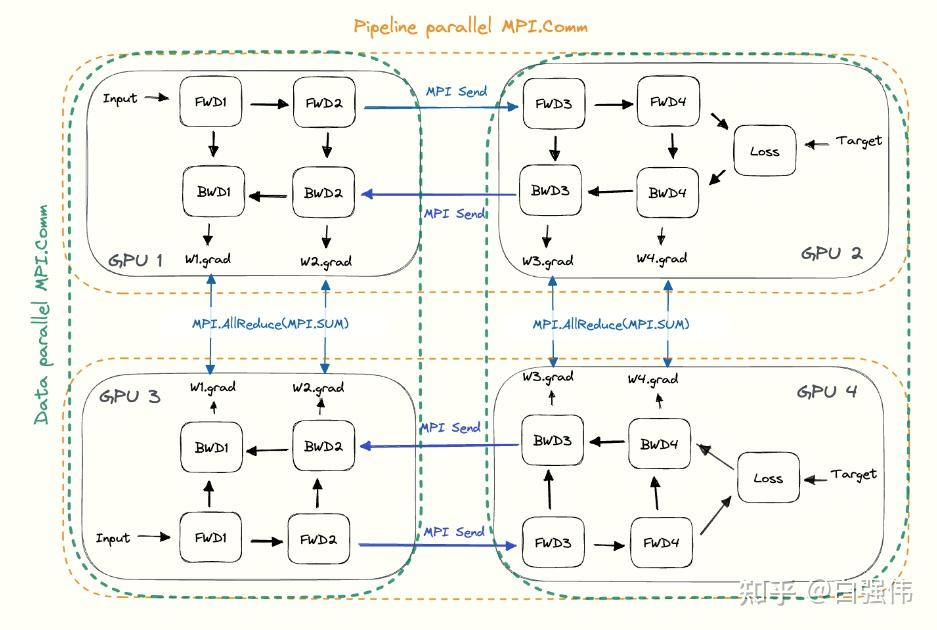
多节点间同 batch 反向传播时的梯度整合(Data parallel 数据并行):
Multi-Token Prediction
关于多 token 预测的另外信息见另一篇文章
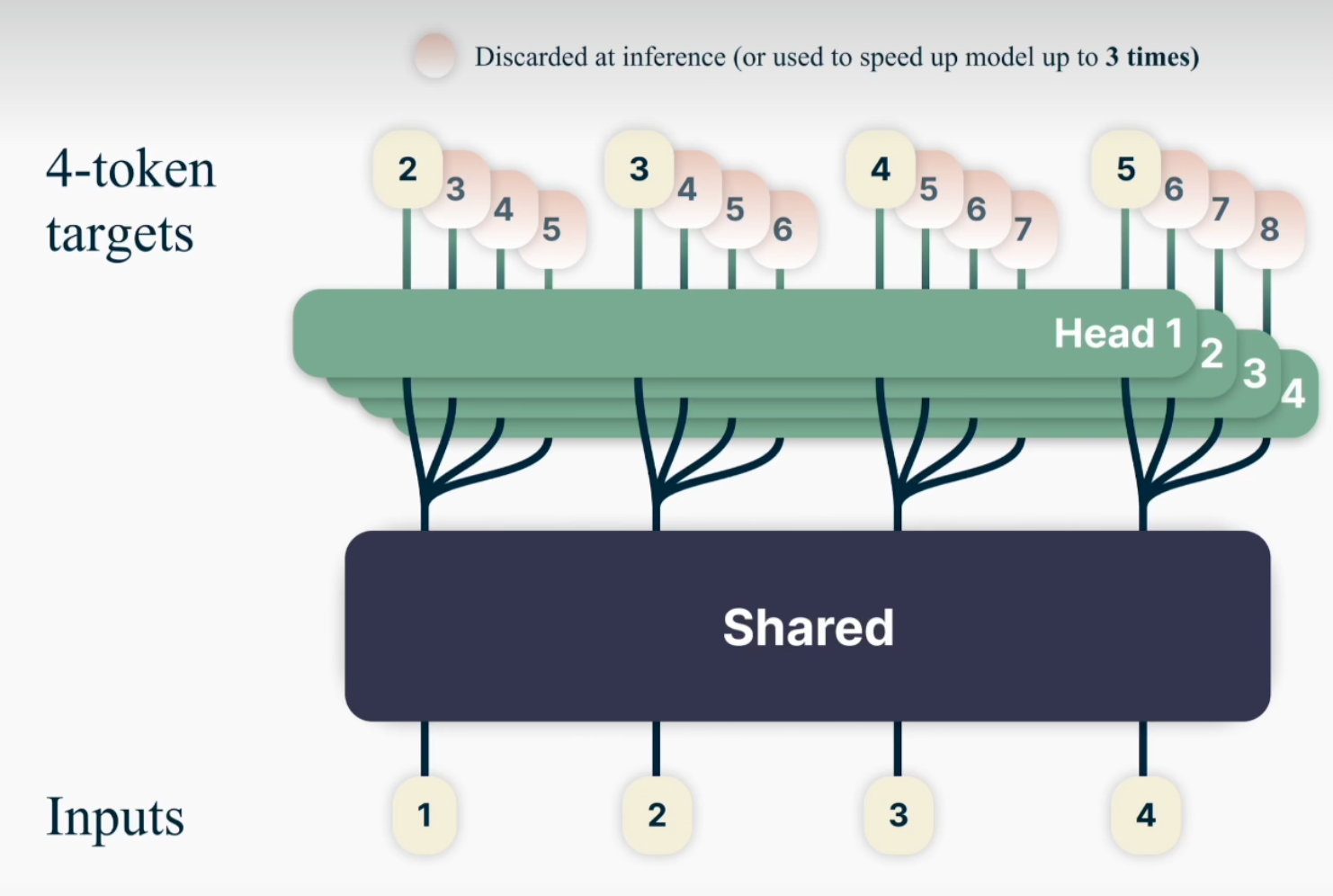
transformer 可以用来做 token 预测,这是当前 LLM 的主要用法。不过经典的用法是 shift 一个 token ,让其可以预测一个 token,而 MTP 机制就是预测之后 n 个 token。如上图, Head 1 负责预测后一个 token(1 预测 2,2 预测 3),Head 2 负责预测后第二个 token(1 预测 3,2 预测 4),以此类推。好处就是信息量更多,训练时的效果可能会更好,同时让模型更加的有”远视”能力,且推理时也会更快更准确。
我们可能会认为这会大大增加训练时间,毕竟 head 数量翻了 n 倍,理论上来说每个 step 会多一些计算量,不过由于这些动作可以并发,实际计算量不会提升特别多。实验证明使用 MTP 方式会加快模型的收敛过程,整体训练效率反而提升。虽然 MTP 的初衷是通过并发推理多个 token 来提升推理时的速度,不过提高训练速度也算是副产物了。
在推理时,也可以并行一次生成多个 token,提高速度,比如 Head 1 由 1 推理 2,head 2 由 1 推理 3,一次就能推理 2 个 token。为了准确性,也能让各个 Head 交叉验证。
但存在的问题是,比如在 Head 2 中,1 直接推理 3,并不符合推理时的 token 的生成逻辑,推理时,token 的预测 shift 是 1,这种联系比较牵强,或者说通过 1 直接推理 3 的做法并不合理。
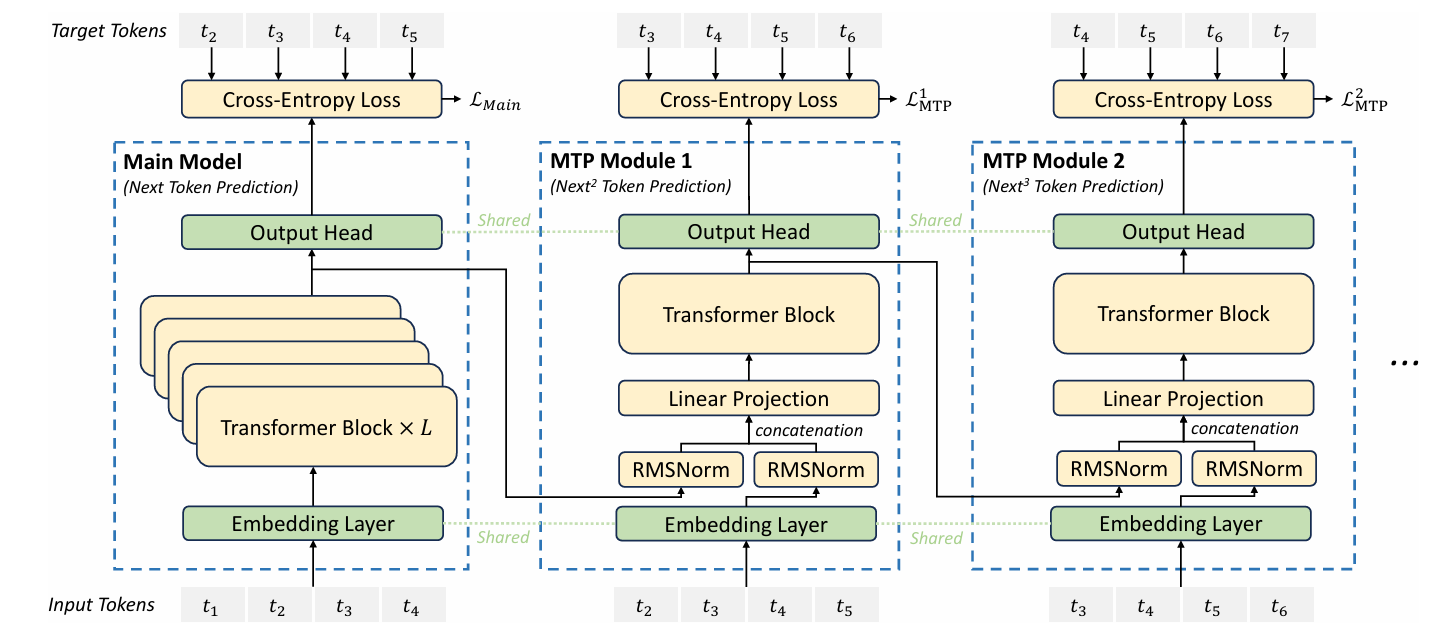
DeepSeek 对 MTP 的改进:
Main Model 就是用来预测下个 token 的主要模型,除了 Main Model 外,训练过程添加了 n 个 MTP Module,它们的参数量都很小,所以对训练速度的影响也较小。比如 MTP Module 1 用来预测后第二个 token ,使用前一个的输出,这样的话,预测 $t_3$ 时,$t_1$ 也能做出贡献,相当于 $t_1$ 预测 $t_3$(shift 2);MTP Module 2 预测 $t_4$ 时,$t_1$, $t_2$ 也能做出贡献,相当于 $t_1$ 预测 $t_4$(shift 3), $t_2$ 预测 $t_4$(shift 2)。MTP Module 2 用来预测后第三个 token,以此类推。这样 MTP 机制中,所有的 shift n 的预测都被训练了。而且对 shift n 个 token 的预测,在每个 MTP Module 看来,前面的 token 都做出了贡献,不像之前的 MTP 在每个 Head 看了都是独立推理的,比如 Head 3 由 1 推理 4,只有 1 做了贡献,2 和 3 没有贡献。
然后再看并发性,之前的 MTP 是完全并发的,4 个 Head 互不影响,而 DeepSeek 的 MTP,则是串行的
这些 MTP Module 的 loss 都会被用来改进 Main Model。
最后推理时,有两种策略:
- 去掉 MTP Module,完全使用 Main Model 进行但 token 预测。
- 像之前的 MTP 一样,让 MTP Module 用于辅助预测,提高并发性。