深度学习学习笔记
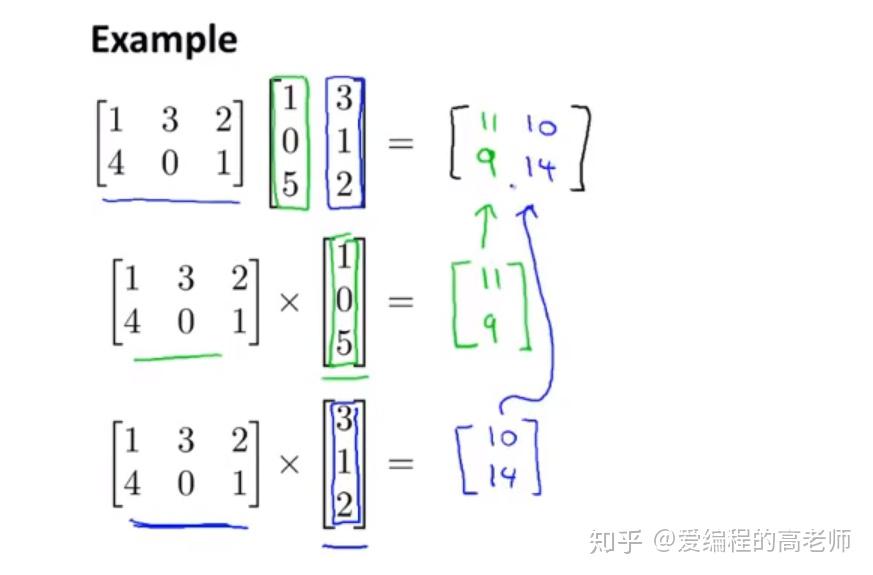
张量
张量(Tensor)表示一个由数值组成的数组,这个数组可能有多个维度:
- 具有一个轴的张量对应数学上的向量(vector);
- 具有两个轴的张量对应数学上的矩阵(matrix);
- 具有两个轴以上的张量没有特殊的数学名称。
运算符
不改变形状:
- 加、减、乘(Hadamard 乘法)、除、求幂(二元)(每个元素独立计算)
- 求自然对数幂(一元)
- 逻辑运算,生成新的 bool 类型张量
改变形状:
- 向量点积($\mathbf{x}^\top \mathbf{y} = \sum_{i=1}^{d} x_i y_i$)
- 矩阵乘法
- 转置($\mathbf{x}^\top$)
- 连结(concatenate):3x4 和 3x5 按照列轴首尾相连,变为 3x9。
- 整体求和,变为单元素
广播(扩展长度为 1 的轴)
numpy 库在进行不同形状的矩阵(必须有一个维度为1)相加时会自动进行广播操作,让它们变成相同形状进行相加
假设形状为
(3,1)和(1,4)的两个矩阵做操作形状为
(3,1)的矩阵:1 2 3 4 5
[ [1], [2], [3] ]
广播后为:
1 2 3 4 5
[ [1, 1, 1, 1], [2, 2, 2, 2], [3, 3, 3, 3] ]
形状为
(1,4)的矩阵:1
[[1, 2, 3 ,4]]
广播后为:
1 2 3 4 5
[ [1, 2, 3, 4], [1, 2, 3, 4], [1, 2, 3, 4] ]
索引
和 python 数组操作差不多,表示范围时左闭右开,用:分隔。例如,[0:2, :]访问第 1 行和第 2 行,其中“:”代表沿轴 1(列)的所有元素。
数据预处理
pandas
数据类型
数据一般会被分为三种类型
连续值(Continuous)、序数值(ordinal)和分类值(categorical values)
连续值
一般用数字表示,具有量化意义,有明确的大小之分,如
100公斤的物品重量大于20公斤的物品,100米要比50米远,一天中的6:00晚于3:00。其中100公斤是20公斤的5倍,称为比例尺度(radio scale)。而不能说6:00是3:00的两倍(可以说6小时是3小时的两倍),或是说6:00加3:00等于9:00,这些运算没有实际意义,它就不是比例尺度。
序数值 比如有小杯、中杯、大杯三个值,我们可以得到关系:大杯>中杯>小杯。注意我们只能对其进行排序,不能进行数值运算,如小杯+中杯等于大杯,或是2倍的中杯等于大杯。
为了进行数学建模,序数值可以映射到整数值,如小杯、中杯、大杯映射到值1、2、3
分类值 比如笼子里有兔子、鸡、狗,它们的地位是完全平等的,无法进行数值计算或是比较。
对分类值进行数学建模有两种方式:
- 标号,将兔子标号为1,鸡标号为2,狗标号为3。存在的问题是标号隐含的大小信息,比如3>2,但由于分类值不能排序,所以会产生误导
- 独热编码(One-Hot Encoding),将兔子标为[1,0,0],鸡标为[0,1,0],狗标为[0,0,1],以上编码是二进制向量,它们之间不能比较,解决了标号带来的隐含大小信息的问题。确定是占用的空间要大于标号。
使用 tensor 表示表格数据
假设有如下表格:
| id | 硫 | … | 品质 |
|---|---|---|---|
| 1 | 110 | … | 8 |
| 2 | 162 | … | 4 |
| 3 | 133 | … | 6 |
以上表格反映了葡萄酒中各种元素(如硫元素、氯化物等)的含量以及对应的酒的品质(由品酒师打分)
首先我们把这个 csv 格式的表格数据加载为 tensor:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
# In[2]:
import csv
wine_path = "../data/p1ch4/tabular-wine/winequality-white.csv"
wineq_numpy = np.loadtxt(wine_path, dtype=np.float32, delimiter=";",
skiprows=1)
wineq_numpy
# Out[2]:
array([[ 7. , 0.27, 0.36, ..., 0.45, 8.8 , 6. ],
[ 6.3 , 0.3 , 0.34, ..., 0.49, 9.5 , 6. ],
[ 8.1 , 0.28, 0.4 , ..., 0.44, 10.1 , 6. ],
...,
[ 6.5 , 0.24, 0.19, ..., 0.46, 9.4 , 6. ],
[ 5.5 , 0.29, 0.3 , ..., 0.38, 12.8 , 7. ],
[ 6. , 0.21, 0.38, ..., 0.32, 11.8 , 6. ]], dtype=float32
其中最后一列是品质,前面都是各种成分的含量,我们把这两个信息分开:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
# In[5]:
data = wineq[:, :-1] # 选取除了最后一列外的所有行列
data, data.shape
# Out[5]:
(tensor([[ 7.00, 0.27, ..., 0.45, 8.80],
[ 6.30, 0.30, ..., 0.49, 9.50],
...,
[ 5.50, 0.29, ..., 0.38, 12.80],
[ 6.00, 0.21, ..., 0.32, 11.80]]), torch.Size([4898, 11]))
# In[6]:
target = wineq[:, -1] # 选取最后一列
target, target.shape
# Out[6]:
(tensor([6., 6., ..., 7., 6.]), torch.Size([4898]))
我们使用独热编码表示品质(当然其实可以使用序号,因为品质分数确实可以排序):
1
2
3
4
5
6
7
8
9
# In[8]:
target_onehot = torch.zeros(target.shape[0], 10)
target_onehot.scatter_(1, target.unsqueeze(1), 1.0)
# Out[8]:
tensor([[0., 0., ..., 0., 0.],
[0., 0., ..., 0., 0.],
...,
[0., 0., ..., 0., 0.],
[0., 0., ..., 0., 0.]])
对成分含量数据进行标准化(也能称为normalize?):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# 求每列的平均值
# In[10]:
data_mean = torch.mean(data, dim=0) # dim表示要缩减的维度,这里0就是行,1就是列。
data_mean
# Out[10]:
tensor([6.85e+00, 2.78e-01, 3.34e-01, 6.39e+00, 4.58e-02, 3.53e+01,
1.38e+02, 9.94e-01, 3.19e+00, 4.90e-01, 1.05e+01])
# 求每列的方差
# In[11]:
data_var = torch.var(data, dim=0)
data_var
# Out[11]:
tensor([7.12e-01, 1.02e-02, 1.46e-02, 2.57e+01, 4.77e-04, 2.89e+02,
1.81e+03, 8.95e-06, 2.28e-02, 1.30e-02, 1.51e+00])
# 标准化:(原始值-平均值)/标准差
# In[12]:
data_normalized = (data - data_mean) / torch.sqrt(data_var)
data_normalized
# Out[12]:
tensor([[ 1.72e-01, -8.18e-02, ..., -3.49e-01, -1.39e+00],
[-6.57e-01, 2.16e-01, ..., 1.35e-03, -8.24e-01],
...,
[-1.61e+00, 1.17e-01, ..., -9.63e-01, 1.86e+00],
[-1.01e+00, -6.77e-01, ..., -1.49e+00, 1.04e+00]])
标准化是为了消除不同种类数据间的量纲差异。首先通过减去平均值让处理后数据的平均值变为 0,再除以标准差进行缩放,让处理后的数据的标准差变为 1。
获取品质最差的条目(小于等于 3 分,一共有20条):
1
2
3
4
5
6
# In[13]:
bad_indexes = target <= 3
bad_indexes.shape, bad_indexes.dtype, bad_indexes.sum()
# Out[13]:
(torch.Size([4898]), torch.bool, tensor(20))
# 输出为一个向量,每个值都是bool,表示对应条目是否满足(target<=3)这个条件
从成分含量数据张量中找出这20条:
1
2
3
4
5
# In[14]:
bad_data = data[bad_indexes]
bad_data.shape
# Out[14]:
torch.Size([20, 11])
以此类推,分别找出好、中、差三个等级的条目:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# In[15]:
bad_data = data[target <= 3]
mid_data = data[(target > 3) & (target < 7)]
good_data = data[target >= 7]
bad_mean = torch.mean(bad_data, dim=0)
mid_mean = torch.mean(mid_data, dim=0)
good_mean = torch.mean(good_data, dim=0)
for i, args in enumerate(zip(col_list, bad_mean, mid_mean, good_mean)):
print('{:2} {:20} {:6.2f} {:6.2f} {:6.2f}'.format(i, *args))
# Out[15]:
0 fixed acidity 7.60 6.89 6.73
1 volatile acidity 0.33 0.28 0.27
2 citric acid 0.34 0.34 0.33
3 residual sugar 6.39 6.71 5.26
4 chlorides 0.05 0.05 0.04
5 free sulfur dioxide 53.33 35.42 34.55
6 total sulfur dioxide 170.60 141.83 125.25
7 density 0.99 0.99 0.99
8 pH 3.19 3.18 3.22
9 sulphates 0.47 0.49 0.50
10 alcohol 10.34 10.26 11.42
我们可以人工分析下,酒的好坏可能和 total sulfur dioxide(二氧化硫) 有关,total sulfur dioxide 的含量约低,酒的品质越高。于是,我们统计 total sulfur dioxide 低于中等品质酒平均值的条目数量,预期能找到好酒:
1
2
3
4
5
6
7
# In[16]:
total_sulfur_threshold = 141.83
total_sulfur_data = data[:,6]
predicted_indexes = torch.lt(total_sulfur_data, total_sulfur_threshold)
predicted_indexes.shape, predicted_indexes.dtype, predicted_indexes.sum()
# Out[16]:
(torch.Size([4898]), torch.bool, tensor(2727))
现在我们把我们预测的“好酒”与实际分数进行对比,首先我们找出 5 分以上的酒:
1
2
3
4
5
# In[17]:
actual_indexes = target > 5
actual_indexes.shape, actual_indexes.dtype, actual_indexes.sum()
# Out[17]:
(torch.Size([4898]), torch.bool, tensor(3258))
然后我们找出我们预测的“好酒”有多少是在这之中的:
1
2
3
4
5
6
7
# In[18]:
n_matches = torch.sum(actual_indexes & predicted_indexes).item()
n_predicted = torch.sum(predicted_indexes).item()
n_actual = torch.sum(actual_indexes).item()
n_matches, n_matches / n_predicted, n_matches / n_actual
# Out[18]:
(2018, 0.74000733406674, 0.6193984039287906)
一共预测对了 61%,这是因为我们只取了其中一个成分做很粗糙的预估。如果使用神经网络统筹所有成分进行评估,正确率会得到质的飞跃。
embedding
我们有个数百万词汇的词汇表,如何将其映射到张量中来作为神经网络的输入呢?首先我们会想到独热编码,但这会导致大量空间浪费。所以需要 embedding 技术。
比如我们现在定义两个维度:颜色和种类,其中颜色维度为 red 且 种类维度为 flower 时,表示罂粟花,其编码就是 {red, flower}。同理,贵宾犬就是 {white, dog}。通过增加更多维度,就能更精确的表示出所有的词汇。而且词义相近的词汇在张量的位置也相近,便于处理。
一方面减少内存的占用,如果用独热编码,那一个单词所占用的空间都是非常夸张的。另一个方面是建立单词间的关联关系。
openai 的 text-embedding-ada-002 模型的输出为 1536 个维度。能够表示多种语言。
线性代数
标量
只有一个元素的张量(0 维),相当于一个点
向量
只有一个轴的张量
维度
张量的轴数量
降维
- 求和,降为标量
- 沿一个轴降维求和,减小一维
- 不降维求和,对应的轴保留维度,即使只剩一个元素
矩阵
只有两个轴的张量
$\mathbf{A} \in \mathbb{R}^{m \times n}$表示(m,n)的矩阵
转置
交换矩阵的行和列
矩阵乘法
可以将第二个矩阵看成是列向量的组合,矩阵和列向量的乘法就是每行向量和列向量的“点积”,然后将结果“连结”
所以要求第一个矩阵的列数必须和第二个矩阵的行数相同。
范数
表示向量的大小
L1 范数:
\[\|\mathbf{x}\|_1 = \sum_{i=1}^n \left|x_i \right|.\]元素绝对值之和
L2 范数:
\[\|\mathbf{x}\|_2 = \sqrt{\sum_{i=1}^n x_i^2},\]元素平方和的平方根,类似于三角不等式求边长和
扩展为 Lp 范数:
\[\|\mathbf{x}\|_p = \left(\sum_{i=1}^n \left|x_i \right|^p \right)^{1/p}.\]矩阵也有类似于向量的范数表示大小的方式
微积分
微分
- 导数:\(f'(x) = \lim_{h \rightarrow 0} \frac{f(x+h) - f(x)}{h}.\)
- 微分运算符:$\frac{d}{dx}$和$D$
- 常见表达式求微分,如幂律
- 法则
偏导数
在多元函数中只对一个变量求导(其余变量视为常数):\(\frac{\partial f}{\partial x_i} = \lim_{h \rightarrow 0} \frac{f(x_1, \ldots, x_{i-1}, x_i+h, x_{i+1}, \ldots, x_n) - f(x_1, \ldots, x_i, \ldots, x_n)}{h}.\)
注意偏导的符号和导数不同
梯度
表示多元函数在某一点上沿每个方向上升或下降的速度(偏导数)。表示为一个向量,每个元素代表一个方向。
函数$f(\mathbf{x})$相对于$\mathbf{x}$($\mathbf{x}=[x_1,x_2,\ldots,x_n]^\top$,转置表示从行向量变为列向量,可以理解为就是函数的参数组)的梯度是一个包含$n$个偏导数的向量:
\[\nabla_{\mathbf{x}} f(\mathbf{x}) = \bigg[\frac{\partial f(\mathbf{x})}{\partial x_1}, \frac{\partial f(\mathbf{x})}{\partial x_2}, \ldots, \frac{\partial f(\mathbf{x})}{\partial x_n}\bigg]^\top,\]梯度也是列向量
关于书中微分多元函数的一些规则,需要参考线性代数中的矩阵-向量积。对于$(m,n)$形状的矩阵 A,乘$x$(列向量,长度为 n),得到的积的表达式为$\nabla_{\mathbf{x}} \mathbf{A} \mathbf{x}$。同理,$\nabla_{\mathbf{x}} \mathbf{x}^\top \mathbf{A}$,表示 x 的转置(变为行向量,长度还是 n)乘矩阵 A 得到的积。
双竖线表示 L2 范数:
$|x|^2$表示$f(x)=x_1^2+x_2^2+…+x_n^2$
梯度为:
$\nabla f(x)=[2x_1+2x_2+…+2x_n]^\top=2[x_1,…,x_n]^\top=2x$
$|\mathbf{x}|_p$表示矩阵的 Frobenius 范数和向量的 L2 范数类似。
链式法则
用于微分复合函数,示例见https://www.cnblogs.com/bigmonkey/p/8350943.html
链式法则可以用于反向传播计算梯度。
自动微分
- 符号微分:直接转换,如 sin(x) 的导数是 cos(x),但也只有特定的表达式能这样转换。
- 数值微分:直接使用微分的方式计算$\frac{dy}{dx}=\frac{f(x+2^{-32})-f(x)}{2^{-32}}$(float32 精度下最小值为$2^{-32}$)。精度越大(如 float64),计算越慢,且占用的内存也越大,但结果也更准确。但这种方式的精度还是无法满足要求,所以在深度学习领域一般只是用来验证梯度计算是否正确。
- 自动微分
梯度保存
pytorch 的 requires_grad 参数用于指定张量是否需要计算梯度(为创建的 tensor 对象预留存储梯度的固定内存区域),而不是每次都分配内存保存计算结果。
梯度下降
在某一点上找下降最快的方向(偏导数最大的方向的反方向)。
反向传播
计算梯度的算法
使用 backward()函数可以对特定的点求其梯度。(注意并不是像我们做题一样推导出导数表达式,而是只对一个点求偏导数)
非标量反向传播
y 也是向量时,不能直接使用 backward()。一般将 y 转为向量的总和,再求梯度
概率
基本概率论
样本(specimen)是观测或调查的一部分个体,总体是研究对象的全部。
选取样本的过程叫做抽样
1
2
3
4
5
# 定义一个向量,长度为6,每个元素表示概率
fair_probs = torch.ones([6]) / 6
# 采样10次,得到采样结果(10个值,样本空间:{0,1,2,3,4,5}),记录索引i在采样结果中出现的次数。比如采样10次,输出结果中的索引0处就是0出现的次数
multinomial.Multinomial(10, fair_probs).sample()
# tensor([0., 1., 2., 4., 2., 1.])
联合概率
多个条件同时发生的概率
贝叶斯定理
A 和 B 同时发生的概率等于 A 发生的概率乘以 A 已经发生时 B 发生的条件概率:
\[P(A, B) = P(B \mid A) P(A)\]同理:
\[P(A, B) = P(A \mid B) P(B)\]得到贝叶斯定理:
\[P(A \mid B) = \frac{P(B \mid A) P(A)}{P(B)}.\]期望
类似加权平均
方差
即平方误差,表示随机变量与其期望的偏差程度。标准差是方差的平方根
线性回归
回归用于预测数值,和分类不同。
目标是在线性模型中找到一组权重向量 w 和偏置 b,让预测值和实际值的偏差尽可能小(损失函数最小)。
损失函数
评估模型的计算值与训练样本中的实际值的差异,训练样本中的实际值是可靠的,所以以它为参考目标,调整模型参数,让模型拟合于训练样本。(前提是训练样本本身确实是可以用模型表示,如果训练样本是完全随机毫无规律的,那也拟合不了)
示例:
我们尝试用线性模型(y = wx + b)进行拟合,我们计算每个点的实际值和拟合值的差距并求和,见解析解,这就是损失函数,通过让这个值变得更小,说明拟合度越高,越接近真实模型。
解析解
见https://zhuanlan.zhihu.com/p/95814925
多元线性回归模型(其中假设 $y$ 为实际向量,$\hat y$ 为预测向量,$\mathbf{X}$为矩阵):
\[\mathbf{\hat y}=\mathbf{X}\mathbf{w}+b\]损失函数 $v$ 可以表示为:
\[v=\|\mathbf{\hat y}-\mathbf{y}\|^2=\|\mathbf{X}\mathbf{w}+b-\mathbf{y}\|^2\]尝试将 b 和 w 合并为 s。对于测试集(一个 y 向量和一个 X 矩阵)中的其中一个结果相关的预测量$\hat y^{(i)}$以及对应参变量$\mathbf{x}$向量($i$为列号):
\[\hat y^{(i)}=w_1x_1^{(i)}+...+w_nx_n^{(i)}+b=s_1x_1^{(i)}+...+s_nx_n^{(i)}+s_{n+1}\]相当于我们将 x 向量视为新的 X 向量,相当于扩充了测试集中的参变量,多加了一列值为 1 的列:
\[\mathbf{X^{(i)}}=[x_1^{(i)},...,x_n^{(i)},1]\]将 w 向量视为新的 s 向量,多加了一个值为 1 的元素:
\[\mathbf{s}=[w_1,...,w_n,b]^\top\]损失函数变为:
\[v=\|\mathbf{\hat y}-\mathbf{y}\|^2=\|\mathbf{X}\mathbf{s}-\mathbf{y}\|^2\]要求损失最小,就是求 $v$ 最小的情况,当然 $v = 0$ 就是最小的,但较难求解,所以通过求导的方式,去求谷底(导数为 0),求$\frac{dv}{ds}=0$时的 s 向量:
\[\mathbf{s} = (\mathbf X^\top \mathbf X)^{-1}\mathbf X^\top \mathbf{y}.\]随机梯度下降
要让损失函数变小,直接方式就是算损失函数关于 w 和 b 的导数(梯度),调整变量(损失函数的变量是 w 权重和 b,而不是 x,y)往偏导数最大的反方向(负梯度)移动。
线性模型比较简单,对其损失函数可以直接推导解析解,甚至不需要训练数据。现在大多数模型都不是线性的(反而还要去线性化),所以梯度下降是更为普遍的做法。
每一个可以移动的方向都由模型参数以及训练样本中的每组 x(训练样本的变量)和 y(训练样本的结果)向量确定,但计算所有方向太慢了,一般每次抽取训练样本中的一部分的 x 和 y,称为小批量随机梯度下降。
极大似然
一般来说线性模型过于理想化,实际的线性模型可能也不是完全线性的,会有一些误差,我们以正态分布误差为例:
\[y = \mathbf{w}^\top \mathbf{x} + b + \epsilon\]可以视为:
\[y = \epsilon\] \[\epsilon \sim \mathcal{N}(\mathbf{w}^\top \mathbf{x} + b, \sigma^2)\]对特定 x 时 y 的似然:
\[P(y \mid \mathbf{x}) = \frac{1}{\sqrt{2 \pi \sigma^2}} \exp\left(-\frac{1}{2 \sigma^2} (y - \mathbf{w}^\top \mathbf{x} - b)^2\right).\]这个表达式中$\mu$就是$\mathbf{w}^\top \mathbf{x} + b$
y 向量的整体匹配概率可以由每个 y 似然连乘得到
极大似然估计和最小化均方误差得到的结果是相同的,都能找到损失最小点。
softmax 回归
softmax 回归有多个输出。在分类问题中,每个输出都表示对应类别与输入的相似度。
如:
- 鸡:0.9
- 狗:0.03
- 鸭:0.3
softmax 就是将相似度转化为分类概率(区别就是分布概率的总和总是为 1):
- 鸡:0.9/(0.9+0.03+0.3)=0.73
是鸡的概率为 73%
由于有多个输出,在全连接的情况下,参数个数为单节点输入数(w 个数)x 总节点数(p)
对数似然
对 softmax 求损失最小的方法也是求最大似然。
损失函数称为交叉熵损失
信息论
softmax 输出信息的熵(熵的意思是包含的信息量)可以用H[P](香农熵)表示。比如上面鸡狗鸭的 softmax 输出概率。
一般来说这个信息的熵就是所有概率相加,就是 1,但是香农熵增加了一个$-\log{P(j)}$,认为概率较低的事件可能让人更惊异(更多信息量)。
所以使用最大似然从信息论的角度看并不完善,我们还要让香农熵中的惊异程度也变小,也就是让香农熵最小。
多层感知机
隐藏层
输入为$\mathbf{X} \in \mathbb{R}^{n \times d}$,表示 n 个样本,每个样本 d 个特征。一层有 h 个输入单元。每个单元权重参数量为 d,与样本特征相同,也就是一层共有$d \times h$个权重参数(偏置 b 也别忘了)。假设单个单元输出的特征个数为 q,该层的输出为$h \times q$。对于分类问题最后要通过输出层(g 个单元)将输出限制为 g 个标量,再通过 softmax 转为每个类别的概率。
注意不管隐藏层有多少,都会退化成一个线性模型,所以必须引入去线性化(激活函数)
过拟合与欠拟合
将数据集分为三份:训练集、验证集、测试集
训练集用于调整模型参数,验证集用于训练过程中识别模型是否过拟合(或欠拟合),测试集用于测试模型的最终效果。
过拟合:在验证集上表现较差,模型泛化能力不足,原因是自由度过高,比如参数量过大、权重取值范围过大,还有样本数量过少。
欠拟合:损失函数无法收敛,模型表达能力不足,可以考虑增加参数量提升复杂度
正则化
为了限制权重取值范围,防止过拟合,使用正则化让所有权重更趋向于 0。当然趋向于任何确定的值都行,比如 1,只是 0 会比较简单。因为 0 正好分割了正数和负数,计算距离时直接使用绝对值,比较简单。
为什么权重取值范围过大会导致过拟合?如果某几个权重很大,远大于其他权重,那么这些权重对应的特征会大幅影响输出结果,导致整个模型偏向于这些权重,可能会偏离正确结果。
正则化就是将参数与 0 的距离也加入损失函数,作为惩罚机制,尽可能使参数趋向于 0。
使用 L2 正则而不是 L1 正则,是为了让通过平方来放大对较大的权重的惩罚,比如[0.1,0.01,3],L1 范数平方为 3.11,L2 范数平方为 9.010001,放大了 3 这个异常值的影响,迫使第三个权重需要再降低,然后第一和第二权重可以适当提高。所以 L2 正则让各个权重更平均,也就是让模型更平滑,单个特征对整个模型的输出影响较小。而 L1 正则让权重整体更趋于 0,但并不一定平滑。
暂退法(Dropout)
用于减少过拟合现象。
在每轮训练中随机抛弃部分中间节点,让结果不过度依赖任何一个节点。注意删除中间节点的同时需要提高其他节点的特征,保证输出结果的数值大小和原来的相似。因为抛弃节点后下一层的输入会少几个特征,需要填补。
比如某一层抛弃 1/2 的节点(输入特征置为 0),则其他节点的输入特征都要乘 2。
前向、反向传播
前向传播
也可以称为推理过程,就是每层的各单元根据输入和自身权重偏置计算结果,并进行一些转换如激活函数、softmax 函数等。得到结果作为下一层的输入,直到得到最终结果。
反向传播
可见文章深度学习-反向传播详解
假设 Z 为输出结果和期望结果的差值(误差),Y 为倒数第一层参数,X 为倒数第二层参数。
我们希望知道 X 对于结果 Z 的影响,也就是倒数第二层的影响,这样可以针对性的调整 X 来得到更正确的结果,方法就是求 Z 对于 X 的偏导数。这个过程就是反向传播,也就是所谓的训练。
根据链式法则,Z 对 X 的偏导数可以由 Z 对 Y 的偏导数推得:
\[\frac{\partial \mathsf{Z}}{\partial \mathsf{X}} = \frac{\partial \mathsf{Z}}{\partial \mathsf{Y}}\frac{\partial \mathsf{Y}}{\partial \mathsf{X}}\]可以看出倒数第二层的偏导数的计算可以利用倒数第一层的偏导数,同理推出计算倒数第三层的梯度时也可以利用这个结果,直到计算完所有层,这就是反向的意思。
一般训练时,每次得到结果后都会计算所有层的参数,并应用梯度下降算法更新所有参数。
反向传播优化
在前向传播过程中,Z 对 Y 以及 Y 对 X 的导数都已经计算过了,可以选择保留下来。这样在反向传播计算 Z 对 X 导数时可以直接使用。
这就导致相比与单纯推理,训练会更耗费内存。
优化器
我们可以手动进行梯度下降,更新模型参数:
\[w = w - \eta \cdot \nabla L(w)\]- $w$: 参数
- $\eta$: 学习率
- $\nabla L(w)$: 损失函数的梯度
有很多方法可以优化这个过程,提高效率:
- 随机梯度下降(SGD,Stochastic Gradient Descent) 每次只随机使用一部分的训练样本计算损失函数并计算梯度,减少计算量。简单稳定。
- 动量法(Momentum) 在参数更新时,引入动量项,利用过去的梯度信息来加速优化,减少震荡。
- AdaGrad(Adaptive Gradient Algorithm) 为每个参数分配独立的学习率,根据历史梯度自适应调整学习率。更新频繁的参数,学习率变小;更新较少的参数,学习率变大。
稳定性
梯度爆炸
梯度过大,参数更新过快,导致难以收敛
梯度消失
梯度过小,参数更新过慢,收敛速度慢。
sigmoid 函数是导致梯度消失的原因之一。在输入很大或很小时导数几乎变 0。结合之前的反向传播链式法则,反向传播过程中如果一个梯度变 0,后续计算的和它相关的梯度就全变 0 了。
而 ReLU 的导数恒为 1,比较稳定。(输入小于 0 时,导数为 0,但输出也为 0,也就是该节点已经失效了,后续输出和该节点没关系,就算梯度消失影响也不大。)
(所以本书之前的例子对权重的初始化都用了均值为 0,方差为 0.01 的正态分布生成)
参数初始化也是需要研究的一门学科。目前深度学习框架都会自动生成,一般不考虑这些。
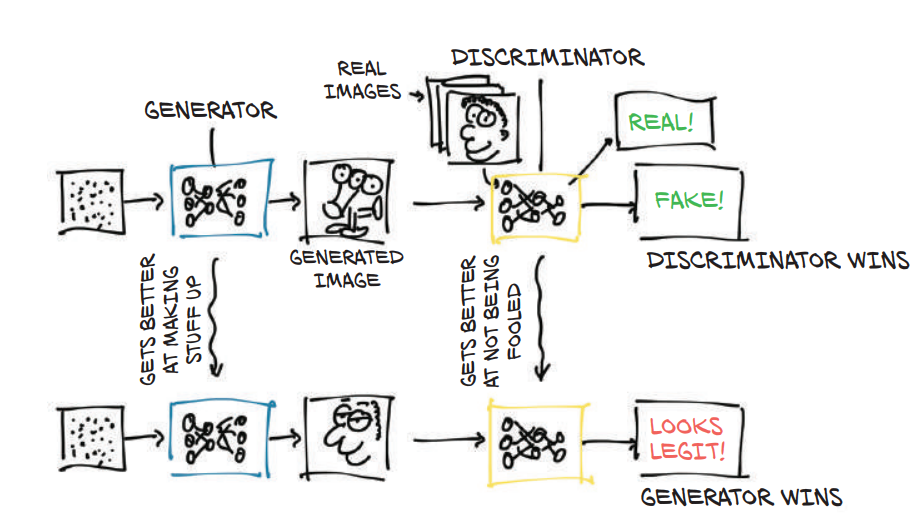
GAN 对抗网络
生成器(generator)与鉴定器(discriminator)的对抗
- 生成器:根据正确图像生成图像(赝品)
- 鉴别器:会随机收到真品和赝品,负责鉴别出是真品还是赝品。
获胜条件:鉴别器鉴定出赝品为赝品,真品为真品,则获胜。鉴别器无法鉴别出赝品为赝品,则失败。
优化过程:失败方需要根据获胜方的意见(即正确率)来调整自身参数,不断优化自身。
结果:生成器能够生成出趋于真品的赝品,鉴别器能识别赝品与真品间的微小差异(不合理的地方,比如 6 根手指)
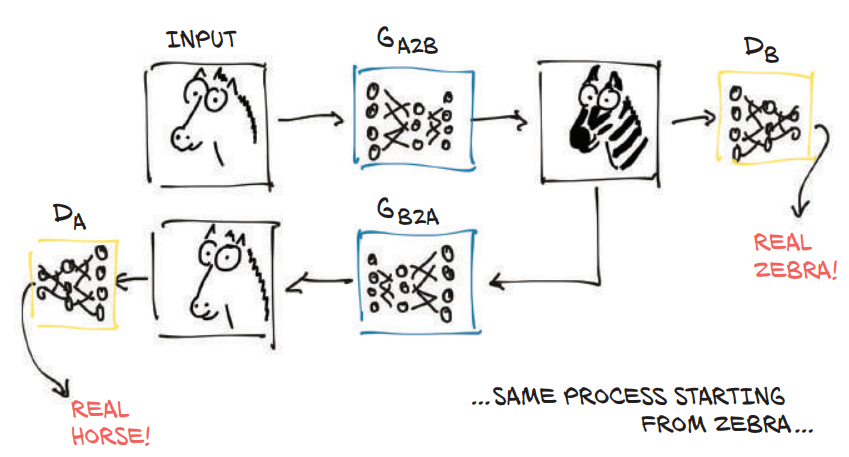
CycleGAN 网络
GAN 网络除了图像生成外,还有一种用途是图像到图像的转换。比如将一张图像转为莫奈风格的画作,将游戏画面转为风格化画面。
- 两个生成器(G 和 F):
- $G$: 将图像从域 $X$ 转换为域 $Y$ 的生成器(如将马的图像转换为斑马)。
- $F$: 将图像从域 $Y$ 转换回域 $X$ 的生成器(如将斑马图像转换回马)。
- 两个判别器($D_X$ 和 $D_Y$):
- $D_X$: 用于判别图像是否属于域 $X$。
- $D_Y$: 用于判别图像是否属于域 $Y$。
其中判别器无需知道也不会关心原始图像的信息(比如马站着还在趴着),其只判断生成器输出图像是否和自身所属域一致(是否伪造)。
- 循环一致性(Cycle Consistency):
- 确保域 $X$ 中的图像 $x$ 在经过转换 $G(x)$ 到域 $Y$ 后,再通过 $F(G(x))$ 返回域 $X$ 时,能尽可能接近原始图像 $x$。
- 类似地,域 $Y$ 中的图像 $y$ 应满足 $F(y) \to G(F(y)) \approx y$。
我们进行图像转换的目的一般是创建风格化的内容,也就是说马转为斑马的过程中,其姿势、形态、大小等都需要一致(语义一致),如果只进行单向的转换,很有可能导致姿势等状态的变化,比如走路的马变成趴着的斑马,和我们预期的不相同。
所有我们引入了反向转换的概念,通过将转换后的图片再反向转换回来,再经过另一个鉴定器$D_X$,同样,它也不会去关心原始图像,只会判断是否符合域 $X$。我们希望通过这种方式来让这个反向转换后的图像接近于原始图像,且保持语义一致,实际上确实可以做到。
训练过程
- 创建一个 resnet 网络,包含随机权重(未训练状态)
- 准备两份数据集:马和斑马
- 进行训练
批次(batch)
一般来说,我们构建模型时参数量会定在一个合理值,比如一次性处理一张图片。
但是在训练过程中,为了能更充分利用 GPU 单元(特别是参数量较小的小模型可能无法用完所有 GPU 单元),会同时进行多个输入,比如同时输入3张图片,相当于同时训练 3 个模型,并行训练并通过一定算法整合训练结果。这就是批次的概念。